题目内容
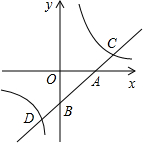
如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数y=-
和y=
的图象交于A点和B点.若C为x轴上任意一点,连接AC,BC,则△ABC的面积为______.

| 3 |
| x |
| 2 |
| x |

设P(0,b),
∵直线AB∥x轴,
∴A,B两点的纵坐标都为b,而点A在反比例函数y=-
的图象上,
∴当y=b,x=-
,即A点坐标为(-
,b),
又∵点B在反比例函数y=
的图象上,
∴当y=b,x=
,即B点坐标为(
,b),
∴AB=
-(-
)=
,
∴S△ABC=
•AB•OP=
•
•b=
.
故答案为:
.
∵直线AB∥x轴,
∴A,B两点的纵坐标都为b,而点A在反比例函数y=-
| 3 |
| x |
∴当y=b,x=-
| 3 |
| b |
| 3 |
| b |
又∵点B在反比例函数y=
| 2 |
| x |
∴当y=b,x=
| 2 |
| b |
| 2 |
| b |
∴AB=
| 2 |
| b |
| 3 |
| b |
| 5 |
| b |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| b |
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |

练习册系列答案
相关题目