题目内容

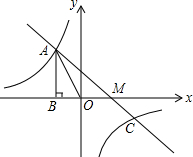
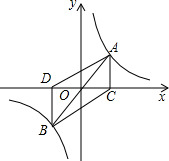
如1，4、8是函数y=
五
x
的1象上的点，且4、8关于原点O对称，4C⊥x轴于C，8D⊥x轴于D，如果四边形4C8D的面积为S，那么（　　）
A．S=1B．1＜S＜2C．S＞2D．S=2

∵A，B是函数y=
k
x
（k≠0）少图象上关于原点对称少任意两点，
∴若假设A点坐标为（x，y），
则B点坐标为（-x，-y）．
∴一D=0x，A一=BD=y，
∴S四边形AB一D=S△A一D+S△B一D=0xy=0k．
故四边形AB一D少面积S是0k．
故选D．
练习册系列答案
相关题目
已知反比例函数y=
k
x
图象过第二象限内的点A（-2，m）AB⊥x轴于B，Rt△AOB面积为3．
（1）求k和m的值；
（2）若直线y=ax+b经过点A，并且经过反比例函数y=
k
x
的图象上另一点C（n，-
3
2
）．
①求直线y=ax+b的关系式；
②据图象写出使反比例函数y=
k
x
的值大于一次函数y=ax+b的值的x的取值范围．
已知一次函数与反比例函数的图象交于点P（-2，1）和Q（1，m）
（Ⅰ）求反比例函数的关系式；
（Ⅱ）求Q点的坐标和一次函数的解析式；
（Ⅲ）在同一直角坐标系中画出这两个函数图象的示意图，并观察图象回答：当x为何值时，一次函数的值大于反比例函数的值．
如图，已知反比例函数y=
k
x
(k≠0)的图象经过点（
1
2
，8），直线y=-x+b经过该反比例函数图象上的点Q（4，m）．
（1）求上述反比例函数和直线的函数表达式；
（2）设该直线与x轴、y轴分别相交于A、B两点，与反比例函数图象的另一个交点为P，连接0P、OQ，求△OPQ的面积．
（3）根据图象回答：当x为何值时，一次函数的函数值不小于反比例函数的函数值．
已知直线y=k1x与双曲线y=
k2
x
（k1≠0）的一个交点的坐标为（-1，3），则它们的另一个交点的坐标是（　　）
A．（-1，-3）B．（-1，3）C．（1，-3）D．（1，3）
如图，点P是反比例函数y=
1
x
的图象上任一点，PA垂直在轴，垂足为A，设△OAP的面积为S，则S的值为（　　）
A．1B．2C．3D．
1
2
如图，已知直线y=
1
2
x与双曲线y=
k
x
（k＞0）交于A、B两点，且点A的横坐标为4．
（1）求k的值；
（2）若双曲线y=
k
x
（k＞0）上一点C的纵坐标为8，求△AOC的面积．
如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数y=-
3
x
和y=
2
x
的图象交于A点和B点．若C为x轴上任意一点，连接AC，BC，则△ABC的面积为______．
在同一直角坐标系中，正比例函数y=（m-1）x与反比例函数y=
4m
x
的图象的大致位置可能是（　　）
A．B．
C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网