题目内容
反比例函数y=
的图象在第一象限如图所示,A点的坐标为(2,2)在双曲线上,是否存在一点B,使△ABO的面积为3?若存在,请求出点B的坐标.

| 4 |
| x |

存在.
设在双曲线y=
上存在点B(m,
),
作AE⊥x轴于E,BF⊥x轴于F,连接OB,
则S△AOE=S△BOF=2,
∵S△AOB=S四边形OABF-S△OBF,
S梯形AEBF=S四边形OABF-S△AOE,
∴S△AOB=S梯形AEFB=3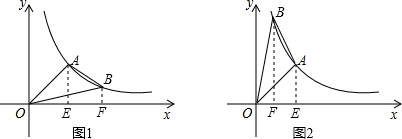
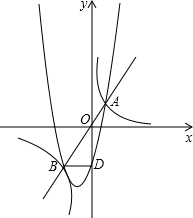
如图1,
=3,
即m2-3m-4=0,
解得,m1=4,m2=-1(舍去),
∴B点坐标(4,1),
如图2,
=3,
即m2+3m-4=0,
解得,m1=-4(舍去),m2=1(舍去),
∴点B坐标为(1,4),
∴点B坐标为(4,1)或(1,4).
设在双曲线y=
| 4 |
| x |
| 4 |
| m |
作AE⊥x轴于E,BF⊥x轴于F,连接OB,
则S△AOE=S△BOF=2,
∵S△AOB=S四边形OABF-S△OBF,
S梯形AEBF=S四边形OABF-S△AOE,
∴S△AOB=S梯形AEFB=3
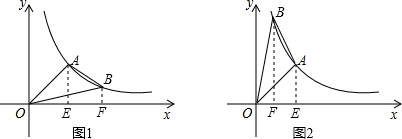
如图1,
(
| ||
| 2 |
即m2-3m-4=0,
解得,m1=4,m2=-1(舍去),
∴B点坐标(4,1),
如图2,
(
| ||
| 2 |
即m2+3m-4=0,
解得,m1=-4(舍去),m2=1(舍去),
∴点B坐标为(1,4),
∴点B坐标为(4,1)或(1,4).

练习册系列答案
相关题目


 B′由直线AB缓慢向下平移;
B′由直线AB缓慢向下平移;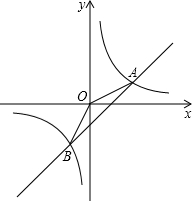 ,n),B(-1,-2).
,n),B(-1,-2).