题目内容

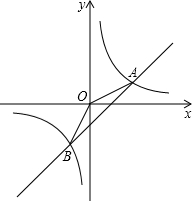
在同一平面直角坐标系中，反比例函数y=-
8
x
与一次函数y=-x+2交于A、B两点，O为坐标原点，求△AOB的面积．
由题意：
y=-
8
x
y-x+2
，解得
x=-2
y=4
，
x=4
y=-2
；
∴A（-2，4）、B（4，-2）．
∵一次函数y=-x+2与y轴的交点坐标C（0，2），
∴OC=2，
∴S△AOB=S△AOC+S△COB=
1
2
×2×2+
1
2
×2×4=6，
综上可得：A、B两点坐标分别为（4，-2）、（-2，4）△AOB的面积为6．
练习册系列答案
相关题目
如图，已知反比例函数y=
k1
x
的图象与一次函数y=k2x+b的图象交于A、B两点，A（2，n），B（-1，-2）．
（1）求反比例函数和一次函数的关系式；
（2）在直线AB上是否存在一点P，使△APO∽△AOB？若存在，求P点坐标；若不存在，请说明理由．
如图，已知直线y=
1
2
x与双曲线y=
k
x
（k＞0）交于A、B两点，且点A的横坐标为4．
（1）求k的值；
（2）若双曲线y=
k
x
（k＞0）上一点C的纵坐标为8，求△AOC的面积．
如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数y=-
3
x
和y=
2
x
的图象交于A点和B点．若C为x轴上任意一点，连接AC，BC，则△ABC的面积为______．
如图，正比例函数y=
1
2
x与反比例函数y=
1
x
在第一象限相交于点A，过点A作x轴的垂线AB，垂足为B，则△AOB的面积为______．
在同一直角坐标系中，正比例函数y=（m-1）x与反比例函数y=
4m
x
的图象的大致位置可能是（　　）
A．B．
C．D．
如图，A、B是双曲线y=
k
x
（k＞0）上的点，A、B两点的横坐标分别为m、2m，线段AB的延长线交x轴于点C，若△AOC的面积为4，则k的值为______．
如图是反比例函数y=
n+3
x
的图象的一支，根据图象回答下列问题：
（1）图象的另一支位于哪个象限？常数n的取值范围是什么？
（2）在图象上取一点P，分别作x轴、y轴的垂线，垂足分别为Q、R，四边形PQOR的面积为3，求n的值．
如图所示，点A（3，n）是反比例函数y=-
6
x
图象上的一点，AB⊥x轴于B，点P是反比例函数y=-
6
x
图象上的一个动点，且S△ABP=4，则点P的坐标是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网