题目内容
【题目】如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证: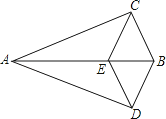
(1)∠CEB=∠CBE;
(2)四边形BCED是菱形
【答案】
(1)
证明:∵△ABC≌△ABD,
∴∠ABC=∠ABD,
∵CE∥BD,
∴∠CEB=∠DBE,
∴∠CEB=∠CBE.
(2)
证明:∵△ABC≌△ABD,
∴BC=BD,
∵∠CEB=∠CBE,
∴CE=CB,
∴CE=BD
∵CE∥BD,
∴四边形CEDB是平行四边形,
∵BC=BD,
∴四边形CEDB是菱形
【解析】(1)欲证明∠CEB=∠CBE,只要证明∠CEB=∠ABD,∠CBE=∠ABD即可.(2)先证明四边形CEDB是平行四边形,再根据BC=BD即可判定. 本题考查全等三角形的性质、菱形的判定、平行四边形的判定等知识,熟练掌握全等三角形的性质是解题的关键,记住平行四边形、菱形的判定方法,属于中考常考题型.

练习册系列答案
相关题目
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息,解答下列问题: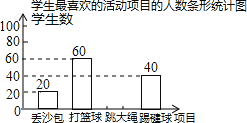
(1)m= , n= , p=;
(2)请根据以上信息直接补全条形统计图;
(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.