题目内容
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1 , y1),B(x2 , y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( ) 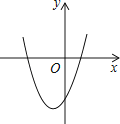
A.y1<y2
B.y1>y2
C.y的最小值是﹣3
D.y的最小值是﹣4
【答案】D
【解析】解:y=x2+2x﹣3=(x+3)(x﹣1),
则该抛物线与x轴的两交点横坐标分别是﹣3、1.
又y=x2+2x﹣3=(x+1)2﹣4,
∴该抛物线的顶点坐标是(﹣1,﹣4),对称轴为x=﹣1.
A、无法确定点A、B离对称轴x=﹣1的远近,故无法判断y1与y2的大小,故本选项错误;
B、无法确定点A、B离对称轴x=﹣1的远近,故无法判断y1与y2的大小,故本选项错误;
C、y的最小值是﹣4,故本选项错误;
D、y的最小值是﹣4,故本选项正确.
故选:D.
【考点精析】根据题目的已知条件,利用二次函数的最值的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.

【题目】某酒店有三人间、双人间客房若干,各种房型每天的收费标准如下:
普通(元/间) | 豪华(元/间) | |
三人间 | 160 | 400 |
双人间 | 140 | 300 |
一个50人的旅游团到该酒店入住,选择了一些三人普通间和双人豪华间入住,且恰好住满.已知该旅游团当日住宿费用共计4020元,问该旅游团入住的三人普通间和双人豪华间各为几间?
【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如表所示
国外品牌 | 国内品牌 | |
进价(万元/部) | 0.44 | 0.2 |
售价(万元/部) | 0.5 | 0.25 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润