题目内容
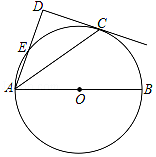
【题目】如图，已知AB‖CD,∠EAF =
∠EAB,∠ECF=∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________
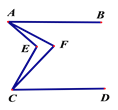
【答案】4∠AFC=3∠AEC
【解析】分析：连接AC，设∠EAF=x°，∠ECF=y°，∠EAB=4x°，∠ECD=4y°，然后根据平行线的性质得出∠AEC=4（x°+y°），∠AFC=3（x°+y°），从而得出答案．
详解：连接AC，设∠EAF=x°，∠ECF=y°，∠EAB=4x°，∠ECD=4y°，
∵AB∥CD，∴∠BAC+∠ACD=180°，∴∠CAE+4x°+∠ACE+4y°=180°，
∴∠CAE+∠ACE=180°-（4x°+4y°），∠FAC+∠FCA=180°-（3x°+3y°）
∴∠AEC=180°-（∠CAE+∠ACE）=180°-[180°-（4x°+4y°）]=4x°+4y°=4（x°+y°），
∠AFC=180°-（∠FAC+∠FCA）=180°-[180°-（3x°+3y°）]=3x°+3y°=3（x°+y°），
∴4∠AFC=3∠AEC．
练习册系列答案
相关题目
【题目】某酒店有三人间、双人间客房若干，各种房型每天的收费标准如下：
普通（元/间） | 豪华（元/间） | |
三人间 | 160 | 400 |
双人间 | 140 | 300 |
一个50人的旅游团到该酒店入住，选择了一些三人普通间和双人豪华间入住，且恰好住满．已知该旅游团当日住宿费用共计4020元，问该旅游团入住的三人普通间和双人豪华间各为几间？
