��Ŀ����
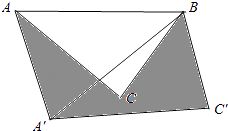
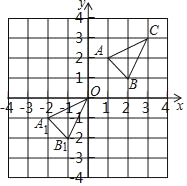
����Ŀ���ڡ�ABC�У�AB=6��AC=BC=5������ABC�Ƶ�A��˳ʱ�뷽����ת���õ���ADE����ת��Ϊ����0�㣼����180�㣩����B�Ķ�Ӧ��Ϊ��D����C�Ķ�Ӧ��Ϊ��E������BD��BE��
��1����ͼ������=60��ʱ���ӳ�BE��AD�ڵ�F��
����֤����ABD�ǵȱ������Σ�
����֤��BF��AD��AF=DF��
����ֱ��д��BE�ij���
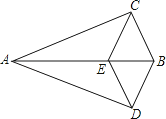
��2������ת�����У�����D��DG��ֱ��ֱ��AB������Ϊ��G������CE������DAG=��ACB�����߶�DG���߶�AE������ʱ����ֱ��д��BE+CE��ֵ��
��ܰ��ʾ���������Ը������⣬�ڱ���ͼ�в���ͼ�Σ��Ա�����
���𰸡�
��1��
�⣺�١ߡ�ABC�Ƶ�A˳ʱ�뷽����ת60��õ���ADE��
��AB=AD����BAD=60�㣬
���ABD�ǵȱ������Σ�
���ɢٵá�ABD�ǵȱ������Σ�
��AB=BD��
�ߡ�ABC�Ƶ�A˳ʱ�뷽����ת60��õ���ADE��
��AC=AE��BC=DE��
�֡�AC=BC��
��EA=ED��
���B��E��AD���д����ϣ�
��BE��AD���д��ߣ�
�ߵ�F��BE���ӳ����ϣ�
��BF��AD��AF=DF��
���ɢ�֪BF��AD��AF=DF��
��AF=DF=3��
��AE=AC=5��
��EF=4��
���ڵȱ�������ABD�У�BF=ABsin��BAF=6�� ![]() =3
=3 ![]() ��
��
��BE=BF��EF=3 ![]() ��4
��4
��2��
�⣺��ͼ��ʾ��

�ߡ�DAG=��ACB����DAE=��BAC��
���ACB+��BAC+��ABC=��DAG+��DAE+��ABC=180�㣬
�֡ߡ�DAG+��DAE+��BAE=180�㣬
���BAE=��ABC��
��AC=BC=AE��
���BAC=��ABC��
���BAE=��BAC��
��AB��CE����CH=HE= ![]() CE��
CE��
��AC=BC��
��AH=BH= ![]() AB=3��
AB=3��
��CE=2CH=8��BE=5��
��BE+CE=13��
����������1��������ת����֪AB=AD����BAD=60�㼴�ɵ�֤������BA=BD��EA=ED�����д������ʼ��ɵ�֤���۷ֱ����BF��EF�ij����ɵã���2���ɡ�ACB+��BAC+��ABC=180�㡢��DAG+��DAE+��BAE=180�㡢��DAG=��ACB����DAE=��BAC�á�BAE=��BAC��AE=AC���������ߺ�һ�ɵ�CE��AB��AC=5��AH=3���̶�֪CE=2CH=8��BE=5�����ɵô𰸣�������Ҫ������ת�����ʡ��ȱ������ε��ж������ʡ��д��ߵ����ʡ��������ڽǺͶ�����֪ʶ�㣬����������ת�������ǽ���Ĺؼ���
�����㾫����������Ĺؼ��������������ε��ڽǺ���ǵ����֪ʶ�����������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ��Լ�����ת�����ʵ����⣬�˽����ת���Ӧ���߶γ��̲��䣬��ת�Ƕȴ�С���䣻����ת���Ӧ�ĵ㵽��ת����ת���ĵľ��벻�䣻����ת�������ͼ�β��䣬ֻ��λ�ñ��ˣ�

����Ŀ��ij�̳����۹��⡢��������Ʒ�Ƶ������ֻ����������ֻ��Ľ��ۺ��ۼ������ʾ
����Ʒ�� | ����Ʒ�� | |
���ۣ���Ԫ/���� | 0.44 | 0.2 |
�ۼۣ���Ԫ/���� | 0.5 | 0.25 |
���̳��ƻ����������ֻ����ɲ�������14.8��Ԫ��Ԥ��ȫ�����ۺ�ɻ�ë����2.7��Ԫ��[ë����=���ۼ۩����ۣ���������]
��1�����̳��ƻ���������Ʒ�ơ�����Ʒ�������ֻ������ٲ���
��2��ͨ���г����У����̳�������ԭ�ƻ��Ļ����ϣ����ٹ���Ʒ���ֻ��Ĺ������������ӹ���Ʒ���ֻ��Ĺ�����������֪����Ʒ���ֻ����ӵ������ǹ���Ʒ���ֻ����ٵ�������3�����������ڹ����������ֻ������ʽ���15.6��Ԫ�����̳�Ӧ������������ʹȫ�����ۺ��õ�ë�������������ë����