题目内容
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
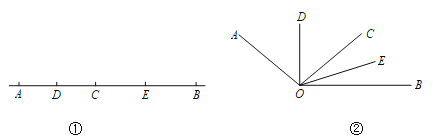
【答案】(1)6cm;(2)6cm;(3)理由见解析;(4)理由见解析.
【解析】试题分析:(1)由中点的定义即可解答;
(2)先求出BC的长,再由中点定义即可解答;
(3)由中点定义可得:DE=![]() AB,只与AB的长有关;
AB,只与AB的长有关;
(4)由角平分线的定义可得:∠DOE=![]() ∠AOB,即可得出结论.
∠AOB,即可得出结论.
试题解析:解:(1)∵AB=12cm,C点为AB的中点,∴AC=BC=6cm.
∵点D、E分别是AC和BC的中点,∴CD=CE=3cm,∴DE=6cm.
(2)∵AB=12cm,AC=4cm,∴BC=8cm.
∵点D、E分别是AC和BC的中点,∴CD=2cm,CE=4cm,∴DE=6cm;
(3)设AC=acm.∵点D、E分别是AC和BC的中点,∴DE=CD+CE=![]() AB=6cm,∴不论AC取何值(不超过12cm),DE的长不变;
AB=6cm,∴不论AC取何值(不超过12cm),DE的长不变;
(4)∵OD、OE分别平分∠AOC和∠BOC,∴∠DOE=∠DOC+∠COE=![]() ∠AOB.
∠AOB.
∵∠AOB=120°,∴∠DOE=60°,∴∠DOE的度数与射线OC的位置无关.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目