题目内容
【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程![]() 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?
经过小组交流讨论后,同学们逐渐形成了两种意见:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.由题意可得a﹣2>0,所以a>2,问题解决.
小强说:你考虑的不全面.还必须保证a≠3才行.
老师说:小强所说完全正确.
请回答:小明考虑问题不全面,主要体现在哪里?请你简要说明: .
完成下列问题:
(1)已知关于x的方程![]() =1的解为负数,求m的取值范围;
=1的解为负数,求m的取值范围;
(2)若关于x的分式方程![]() =﹣1无解.直接写出n的取值范围.
=﹣1无解.直接写出n的取值范围.
【答案】(1):m<![]() 且m≠﹣
且m≠﹣![]() ;(2)n=1或n=
;(2)n=1或n=![]() .
.
【解析】
考虑分式的分母不为0,即分式必须有意义;
(1)表示出分式方程的解,由解为负数确定出m的范围即可;
(2)分式方程去分母转化为整式方程,根据分式方程无解,得到有增根或整式方程无解,确定出n的范围即可.
请回答:小明没有考虑分式的分母不为0(或分式必须有意义)这个条件;
(1)解关于x的分式方程得,x=![]() ,
,
∵方程有解,且解为负数,
∴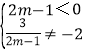 ,
,
解得:m<![]() 且m≠-
且m≠-![]() ;
;
(2)分式方程去分母得:3-2x+nx-2=-x+3,即(n-1)x=2,
由分式方程无解,得到x-3=0,即x=3,
代入整式方程得:n=![]() ;
;
当n-1=0时,整式方程无解,此时n=1,
综上,n=1或n=![]() .
.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目