��Ŀ����
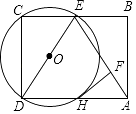
����Ŀ����֪����ͼ��������y=ax2+bx+c��x�ύ��������ͬ�ĵ�A����4��0����B��1��0������y�������ύ�ڵ�C��tan��CAB= ![]() ��
��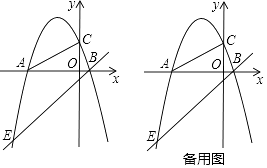
��1���������ߵĽ���ʽ����֤��Q����1��3���Ƿ����������ϣ�
��2����M���߶�AC��һ���㣨����A��C�غϣ�������M��x��Ĵ��ߣ�����ΪH�����������ڵ�N�����жϵ�MNΪ���ֵʱ����MNΪֱ����Բ��y���λ�ù�ϵ��˵�����ɣ�
��3����֪����B��ֱ��y=x��1������������һ��E���ʣ���x�����Ƿ���ڵ�P��ʹ�Ե�P��A��QΪ��������������AEB���ƣ������ڣ���������з���Ҫ��ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��Rt��AOC�У���COA=90�㣬AO=4��tan��CAB= ![]() ��
��
��OC=2��
��C��0��2����
�������ߵĽ���ʽΪy=a��x+4����x��1��������C���������ã���4a=2�����a=�� ![]() ��
��
�������ߵĽ���ʽΪy=�� ![]() ����x2+3x��4������y=��
����x2+3x��4������y=�� ![]() x2��
x2�� ![]() x+2��
x+2��
��x=1ʱ��y=�� ![]() ������1��2��
������1��2�� ![]() ������1��+2=3��
������1��+2=3��
���Q����1��3������������
��2��
�⣺��ͼ1��ʾ��
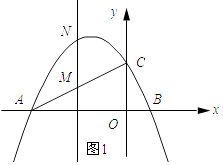
��ֱ��AC�Ľ���ʽΪy=kx+b������A��C���������ã� ![]() ��
��
��ã�k= ![]() ��b=2��
��b=2��
��ֱ��AC�Ľ���ʽΪy= ![]() x+2��
x+2��
���M��������m�� ![]() m+2�������N��m����
m+2�������N��m���� ![]() m2��
m2�� ![]() m+2����
m+2����
��MN=�� ![]() m2��
m2�� ![]() m+2����
m+2���� ![]() m+2��=��
m+2��=�� ![]() ��m+2��2+2��
��m+2��2+2��
�൱m=��2ʱ��MN�����ֵΪ2��
����MNΪֱ����Բ�İ뾶Ϊ1��
�֡���MNΪֱ����Բ��Բ�ĵ�y��ľ���Ϊ2��
����MNΪֱ����Բ��y������
��3��
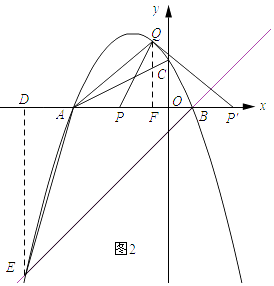
�⣺��ͼ2��ʾ������E��ED��x�ᣬ����ΪD������Q��QF��x�ᣬ����ΪF��
��y=x��1��y=�� ![]() x2��
x2�� ![]() x+2��������ã�x=��6��y=��7��x=1��y=0��
x+2��������ã�x=��6��y=��7��x=1��y=0��
���E����������6����7����
��BD=ED=7��
�֡ߡ�EDB=90��
���EBD=45�㣮
ͬ����QAF=45�㣮
���EBD=��QAF=45�㣮
���QAD=135�㣬90�㣼��EAB��135�㣮
���Pֻ���ڵ�A���Ҳ࣮
���������ľ��빫ʽ��֪��EB=7 ![]() ��AQ=3
��AQ=3 ![]() ��AB=5��
��AB=5��
����QAP��ס�ABEʱ���� ![]() ����
���� ![]() =
= ![]() �����AP��=
�����AP��= ![]() ��
��
��OP��= ![]() ��4=
��4= ![]() ��
��
������AQP�ס�BEAʱ���� ![]() ����
���� ![]() ����ã�AP=
����ã�AP= ![]() ��
��
��OP=5�� ![]() =
= ![]() ��
��
���P���������� ![]() ��0����
��0���� ![]() ��0��
��0��
����������1������������Ǻ����Ķ�������OC=2���Ӷ��õ���C��0��2�����������ߵĽ���ʽΪy=a��x+4����x��1��������C�������������a��ֵ���Ӷ��ɵõ������ߵĽ���ʽ��Ȼ�����ݵ�Q�������Ƿ���������ߵĽ���ʽ��֪��Q�Ƿ����������ϣ���2�������ֱ��AC�Ľ���ʽ�����M������Ϊ��m�� ![]() m+2�������N��m����
m+2�������N��m���� ![]() m2��
m2�� ![]() m+2����Ȼ���г�MN�ij�����m�ĺ����Ĺ�ϵʽ�������䷽�������MN�����ֵ�Լ���ʱm��ֵ��Ȼ������d��r�Ĺ�ϵ���ж�����MNΪֱ����Բ��y���λ�ù�ϵ����3������E��ED��x�ᣬ����ΪD������Q��QF��x�ᣬ����ΪF������õ�E�����꣬Ȼ���֤����DBE�͡�AQF��Ϊ����ֱ�������Σ��ʴ��ڡ�BAE�͡�AQP�У���QAP=��ABE��Ȼ�����������ľ��빫ʽ���EB��AQ��AB�ij���Ȼ���Ϊ��QAP��ס�ABE����AQP�ס�BEA���������⼴�ɣ�
m+2����Ȼ���г�MN�ij�����m�ĺ����Ĺ�ϵʽ�������䷽�������MN�����ֵ�Լ���ʱm��ֵ��Ȼ������d��r�Ĺ�ϵ���ж�����MNΪֱ����Բ��y���λ�ù�ϵ����3������E��ED��x�ᣬ����ΪD������Q��QF��x�ᣬ����ΪF������õ�E�����꣬Ȼ���֤����DBE�͡�AQF��Ϊ����ֱ�������Σ��ʴ��ڡ�BAE�͡�AQP�У���QAP=��ABE��Ȼ�����������ľ��빫ʽ���EB��AQ��AB�ij���Ȼ���Ϊ��QAP��ס�ABE����AQP�ס�BEA���������⼴�ɣ�

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�