题目内容
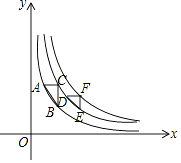
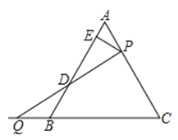
【题目】如图，△ABC 是边长为 6 cm 的等边三角形，P 从点 A 岀发沿 AC 边向 C 运动， 与此同时 Q 从 B 出发以相同的速度沿 CB 延长线方向运动．当 P 到达 C 点时，P、Q 停止运动， 连接 PQ 交 AB 于 D
（1）设 P、Q 的运动速度为 1 cm/s，当运动时间为多少时，∠BQD＝30°？
（2）过 P 作 PE⊥AB 于 E，在运动过程中线段 ED 的长是否发生变化？如果不变，求出线段 ED的长；如果变化请说明理由
【答案】(1) 运动时间为2s;(2) ED 的长不会发生变化，DE=3.
【解析】
(1) 根据三角形内角和为180
, 可知△PQC为直角三角形, 根据特殊角的三角函数值即可求出AP的长后可得时间.
(2) 根据全等三角形的角角边判定定理可得,Rt△ABE≌Rt△BQF,再由全等三角形对应边相等可知:AE=BF,EP=QF, 因为EP//QF, 可知四边形EPFQ是平行四边形, 根据平行四边形对角线互相平分可得: DE=
EF.EB+AE=BE+BF=AB,DE=AB., 由于△ABC是不变的, AB是定长, 即可证明当点P、 Q运动时, 线段DE的长度不会改变.
解：(1)
△ABC是边长为6的等边三角形,
∠ACB=60.
∠BQD=30,∠QPC=90.
设AP=x,则PC=6-x,QB=x,
QC=QB+BC=6+x，PC=AC-AP=6-x，
在Rt△QCP中, ∠BQD=30,
PC=QC,即6-x= (6+x),
解得x=2，
又 P、Q 的运动速度为 1 cm/s，
运动的时间为2s；
(2) 当点P、 Q运动时, 线段ED的长度不会改变.理由如下:作QF⊥AB, 交直线AB的延长线于点F,连接QE,PF.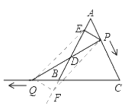
PE⊥AB于E,∠DFQ=∠AEP=90.
点P、Q做匀速运动且速度相同,AP=BQ.
△ABC是等边三角形,
∠A=∠ABC=∠FBQ=60.
在△APE和△BQF中,
∠A=∠FBQ,AP=BQ,∠AEP=∠BFQ=90,
△APE≌△BQF (AAS).
AE=BF,PE=QF且PE∥QF.
四边形PEQF是平行四边形。
DE=EF.
EB+AE=BE+BF=AB,
DE=AB.
又等边△ABC的边长为6, DE=3.
当点P、Q运动时, 线段ED的长度不会改变.
