题目内容
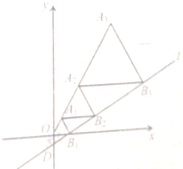
【题目】“赵爽炫图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽炫图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为
,较短直角边长为
，若(a+b)2=21，大正方形的面积为13，则小正方形的边长为( )
A. 
B. 2 C. 
D. 
【答案】C
【解析】观察图形可知，小正方形的面积=大正方形的面积-4个直角三角形的面积，利用已知（a+b）2=21，大正方形的面积为13，可以得出直角三角形的面积，进而求出小正方形的面积，即可得出小正方形的边长．
解：∵(a+b)2=21，
∴a2+2ab+b2=21，
∵大正方形的面积为13，
2ab=2113=8，
∴小正方形的面积为138=5.
∴小正方形的边长为
.
故选：C.
【题目】某校七年级各班分别选出3名学生组成班级代表队，参加知识竞赛，得分最多的班级为优胜班级，各代表队比赛结果如下：
班级 | 七（1） | 七（2） | 七（3） | 七（4） | 七（5） | 七（6） | 七（7） | 七（8） | 七（9） | 七（10） |
得分 | 85 | 90 | 90 | 100 | 80 | 100 | 90 | 80 | 85 | 90 |
（1）写出表格中得分的众数、中位数；
（2）学校从获胜班级的代表队中各抽取1名学生组成“绿色环保监督”小组，小明、小红分别是七（4）班和七（6）班代表队的学生，用列表法或画树状图的方法说明同时抽到小明和小红的概率是多少？
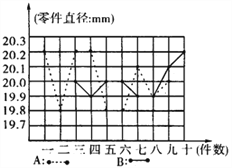
【题目】为选派一名学生参加全市实践活动技能竞赛，A，B两位同学在校实习基地现场进行加工直径为20mm的零件的测试，他俩加工的10个零件的相关数据依次如下图表所示（单位：mm）．
根据测试得到的有关数据，试解答下列问题：
平均数 | 方差 | 完全符合要求的个数 | |
A | 20 | 0.026 | 2 |
B | 20 | S2B | 5 |
（1）考虑平均数与完全符合要求的个数，你认为________的成绩好些．
（2）计算出S2B的大小，考虑平均数与方差，说明谁的成绩好些．
（3）考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你的理由．