题目内容
【题目】如图，点A，C，D，E在Rt△MON的边上，∠MON=90°，AE⊥AB且AE=AB，BC⊥CD，BH⊥ON于点H，DF⊥ON于点F，OM=12，OE=6，BH=3，DF=4，FN=8，图中阴影部分的面积为（ ）
A. 30 B. 50 C. 66 D. 80
【答案】B
【解析】
易证△AEO≌△BAH，△BCH≌△CDF即可求得AO=BH，AH=EO，CH=DF，BH=CF，即可求得梯形DEOF的面积和△AEO，△ABH，△CGH，△CDF的面积，即可解题．
∵∠EAO+∠BAH=90°，∠EAO+∠AEO=90°，
∴∠BAH=∠AEO，
∵在△AEO和△BAH中，
，
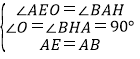∴△AEO≌△BAH（AAS），
同理△BCH≌△CDF（AAS），
∴AO=BG=3，AH=EO=6，CH=DF=4，BH=CF=3，
∵梯形DEOF的面积=
（EF+DH）FH=80，
S△AEO=S△ABH=AFAE=9，
S△BCH=S△CDF=CHDH=6，
∴图中实线所围成的图形的面积S=80-2×9-2×6=50，
故选B．
练习册系列答案
相关题目
