题目内容
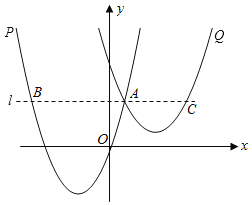
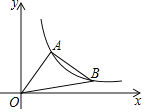
【题目】如图,横坐标为1的点A在反比例函数y=![]() 上(x>0)的图象上,将线段AO绕着点A逆时针旋转90°得到线段AB,且点B也落在反比例函数y=
上(x>0)的图象上,将线段AO绕着点A逆时针旋转90°得到线段AB,且点B也落在反比例函数y=![]() (x>0)的图象上
(x>0)的图象上
(1)求反比例函数的解析式;
(2)求线段AO扫过的面积.
【答案】(1)y=![]() ;(2)
;(2)![]() π.
π.
【解析】
(1)过A作AE⊥x轴,过B作BD⊥AE,利用同角的余角相等得到一对角相等,再由一对直角相等,且AO=AB,利用AAS得出三角形AOE与三角形ABD全等,由确定三角形的对应边相等得到BD=AE=m,AD=OE=1,进而表示出ED及OE+BD的长,即可表示出B坐标;由A与B都在反比例图象上,得到A与B横纵坐标乘积相等,列出关系式,于是得到结论;
(2)根据扇形的面积公式即可得到结论.
(1)过A作AE⊥x轴,过B作BD⊥AE.设AE= m.
∵∠OAB=90°,∴∠OAE+∠BAD=90°.
∵∠AOE+∠OAE=90°,∴∠BAD=∠AOE.
在△AOE和△BAD中,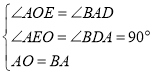 ,∴△AOE≌△BAD(AAS),∴AE=BD=m,OE=AD=1,∴DE=m﹣1,OE+BD=m+1,则B(m+1,m﹣1).
,∴△AOE≌△BAD(AAS),∴AE=BD=m,OE=AD=1,∴DE=m﹣1,OE+BD=m+1,则B(m+1,m﹣1).
∵A与B都在反比例图象上,得到m=(m+1)(m﹣1),解得:m![]() (负值舍去),∴A(1,
(负值舍去),∴A(1,![]() ),∴k
),∴k![]() ,∴反比例函数的解析式为:y
,∴反比例函数的解析式为:y![]() ;
;
(2)∵OE=1,AE![]() ,∴OA
,∴OA![]() ,∴线段AO扫过的面积
,∴线段AO扫过的面积![]() π.
π.

练习册系列答案
相关题目