题目内容
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣mx+n.
(1)当m=2时,
①求抛物线的对称轴,并用含n的式子表示顶点的纵坐标;
②若点A(﹣2,y1),B(x2,y2)都在抛物线上,且y2>y1,则x2的取值范围是 ;
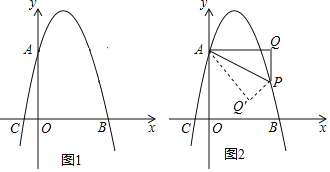
(2)已知点P(﹣1,2),将点P向右平移4个单位长度,得到点Q.当n=3时,若抛物线与线段PQ恰有一个公共点,结合函数图象,求m的取值范围.
【答案】(1)①n﹣1;②x2<﹣2或x2>4;(2)m≤﹣2或m=2或![]() .
.
【解析】
(1)①把m=2代入抛物线解析式,利用x=![]() ,求出对称轴,然后把顶点横坐标代入,即可用含n的式子表示出顶点的纵坐标;
,求出对称轴,然后把顶点横坐标代入,即可用含n的式子表示出顶点的纵坐标;
②利用抛物线的对称性,及开口向上,可知离对称轴越远,函数值越大,从而可解;
(2)把n=3代入,再分抛物线经过点Q,抛物线经过点P(1,2),抛物线的顶点在线段PQ上,三种情况分类讨论,得出相应的m值,从而得结论.
解:(1)①∵m=2,
∴抛物线为y=x2﹣2x+n.
∵x![]() 1,
1,
∴抛物线的对称轴为直线x=1.
∵当线x=1时,y=1﹣2+n=n﹣1,
∴顶点的纵坐标为:n﹣1.
②∵抛物线的对称轴为直线x=1,开口向上,
x=﹣2到x=1的距离为3,
∴点A(﹣2,y1),B(x2,y2)都在抛物线上,且y2>y1,则x2的取值范围是x2<﹣2或x2>4,
故答案为:x2<﹣2或x2>4.
(2)∵点P(﹣1,2),向右平移4个单位长度,得到点Q.
∴点Q的坐标为(3,2),
∵n=3,
抛物线为y=x2﹣mx+3.
当抛物线经过点Q(3,2)时,2=32﹣3m+3,解得![]() ;
;

当抛物线经过点P(﹣1,2)时,2=(﹣1)2+m+3,解得m=﹣2;
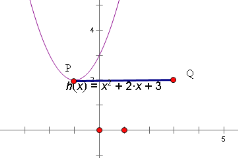
当抛物线的顶点在线段PQ上时,![]() 2,解得m=±2.
2,解得m=±2.
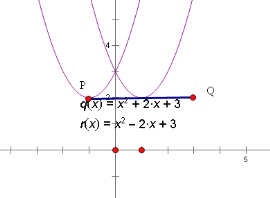
结合图象可知,m的取值范围是m≤﹣2或m=2或![]() .
.
故答案为:m≤﹣2或m=2或![]() .
.