题目内容
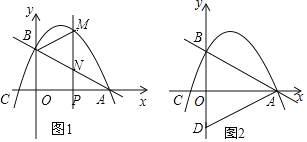
【题目】如图,抛物线P:![]() 与抛物线Q:
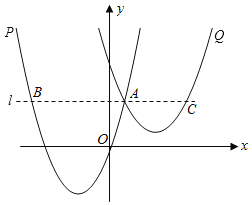
与抛物线Q:![]() 在同一平面直角坐标系中(其中a,t均为常数,且t>0),已知点A(1,3)为抛物线P上一点,过点A作直线l∥x轴,与抛物线P交于另一点B.
在同一平面直角坐标系中(其中a,t均为常数,且t>0),已知点A(1,3)为抛物线P上一点,过点A作直线l∥x轴,与抛物线P交于另一点B.
(1)求a的值及点B的坐标;
(2)当抛物线Q经过点A时
①求抛物线Q的解析式;
②设直线l与抛物线Q的另一交点为C,求![]() 的值.
的值.
【答案】(1)a=![]() ,B(﹣5,3);(2)①y2=
,B(﹣5,3);(2)①y2=![]() (x﹣3)2+1;②
(x﹣3)2+1;②![]() .
.
【解析】
(1)先利用待定系数法求出抛物线P的解析式,即可得出结论;
(2)①利用待定系数法求出抛物线Q的解析式,即可得出结论;
②先求出AC,AB,即可得出结论.
(1)∵抛物线P:y1=a(x+2)2﹣3过点A(1,3),∴9a﹣3=3,∴a![]() ,∴抛物线P:y1
,∴抛物线P:y1![]() (x+2)2﹣3.
(x+2)2﹣3.
∵l∥x轴,∴点B的纵坐标为3,∴3![]() (x+2)2﹣3,∴x=1(点A的横坐标)或x=﹣5,∴B(﹣5,3);
(x+2)2﹣3,∴x=1(点A的横坐标)或x=﹣5,∴B(﹣5,3);
(2)①如图,∵抛物线Q:y2![]() (x﹣t)2+1过点A(1,3),∴
(x﹣t)2+1过点A(1,3),∴![]() (1﹣t)2+1=3,∴t=﹣1(舍)或t=3,∴抛物线Q:y2
(1﹣t)2+1=3,∴t=﹣1(舍)或t=3,∴抛物线Q:y2![]() (x﹣3)2+1;
(x﹣3)2+1;
②∵l∥x轴,∴点C的纵坐标为3,∴3![]() (x﹣3)2+1,∴x=1(点A的横坐标)或x=5,∴C(5,1),∴AC=5﹣1=4.
(x﹣3)2+1,∴x=1(点A的横坐标)或x=5,∴C(5,1),∴AC=5﹣1=4.
∵A(1,3),B(﹣5,3),∴AB=1﹣(﹣5)=6,∴![]() .
.

【题目】某校为改善办学条件,计划购进![]() 两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
A | 240 | 0 | 210 | 20 |
B | 300 | 0 | 250 | 30 |
(Ⅰ)如果在线下购买![]() 两种书架20个,共花费5520元,求
两种书架20个,共花费5520元,求![]() 两种书架各购买了多少个;
两种书架各购买了多少个;
(Ⅱ)如果在线上购买![]() 两种书架20个,共花费
两种书架20个,共花费![]() 元,设其中
元,设其中![]() 种书架购买
种书架购买![]() 个,求W关于
个,求W关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)在(Ⅱ)的条件下,若购买![]() 种书架的数量不少于
种书架的数量不少于![]() 种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.
种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.