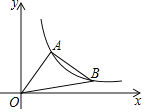
题目内容
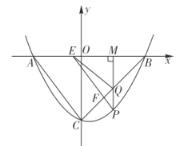
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 是第四象限内抛物线上的一个动点,过点
是第四象限内抛物线上的一个动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求抛物线 ![]() 的解析式;
的解析式;
(2)求![]() 面积的最大值;
面积的最大值;
(3)① 试探究在点![]() 的运动过程中,是否存在这样的点
的运动过程中,是否存在这样的点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形? 若存在,请求出此时点
为顶点的三角形是等腰三角形? 若存在,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
② 请直接写出当![]() 等腰直角三角形时,点
等腰直角三角形时,点![]() 的坐标 .
的坐标 .
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①点
;(3)①点![]() 的坐标为
的坐标为![]() 或
或![]() ,②点
,②点![]() 的坐标为
的坐标为![]()
【解析】
(1)根据抛物线经过A、B两点和![]() 可得点C坐标,从而利用待定系数法求出抛物线表达式;
可得点C坐标,从而利用待定系数法求出抛物线表达式;
(2)求出AC和BC的表达式,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,得出当
,得出当![]() 最大时,
最大时,![]() 最大,设点
最大,设点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),将PQ用关于t的式子表示出来,求出PQ的最大值即可得到
),将PQ用关于t的式子表示出来,求出PQ的最大值即可得到![]() 的最大值;
的最大值;
(3)①设点![]() 的坐标为
的坐标为![]() ,分AC=AQ,AC=CQ两种情况,结合等腰三角形的性质求出点Q坐标即可;
,分AC=AQ,AC=CQ两种情况,结合等腰三角形的性质求出点Q坐标即可;
②设点![]() 的坐标为
的坐标为![]() ,证明△AOC∽△EMP,表示出EM和QM,建立方程,解之即可.
,证明△AOC∽△EMP,表示出EM和QM,建立方程,解之即可.
解:(1)抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,
∴![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
∴![]() .
.
∴![]() ,
,
解得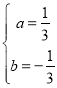 ,
,
∴ 抛物线的解析式为![]() ;
;
(2) ∵ 点![]() ,
,
∴ 直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() ,
,
∴ 直线![]() 的解析式为
的解析式为![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
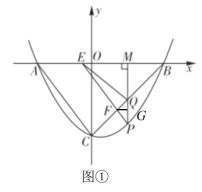
如图,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴ 当![]() 最大时,
最大时,![]() 最大 ,
最大 ,
设点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),
),
则 ![]() ,
,
∴![]() ,
,
当![]() 时,
时, ![]() 最大值为
最大值为![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)① 存在,设点![]() 的坐标为
的坐标为![]() ,
,
则![]() .
.
如图,当![]() 时,有
时,有![]() ,
,
解得 ![]() =0 (舍),
=0 (舍),
![]() =1 ,此时点
=1 ,此时点![]() 的坐标为
的坐标为![]() ;
;
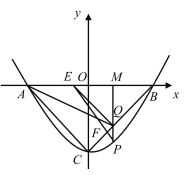
如图,当![]() 时,
时,
![]() ,有
,有![]()
解得,![]() (舍),
(舍),![]() ,
,
此时点![]() 的坐标为
的坐标为![]() ,
,
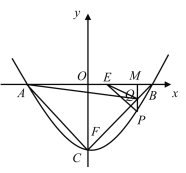
综上,以 ![]() 为顶点的三角形是等腰三角形时,点
为顶点的三角形是等腰三角形时,点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
②当△EMQ为等腰直角三角形时,设点![]() 的坐标为
的坐标为![]() ,
,
∴点P坐标为(![]() ,
,![]() ),
),
∵PE∥AC,
∴可得△AOC∽△EMP,
则![]() ,
,
∴EM=![]() ,
,
∵EM=QM,
∴![]() =4-n,
=4-n,
解得:n=1或n=4(舍),
∴点![]() 的坐标为
的坐标为![]() .
.