题目内容
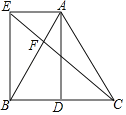
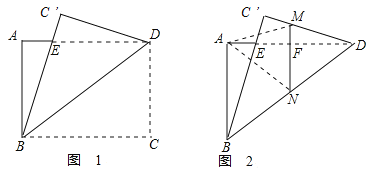
【题目】在矩形![]() 中,
中,![]() ,将其沿对角线
,将其沿对角线![]() 折叠,顶点
折叠,顶点![]() 的对应点
的对应点![]() ,
,![]() 交
交![]() 于点
于点![]() 如图1,再折叠,使点
如图1,再折叠,使点![]() 落在
落在![]() 处,折痕
处,折痕![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,得到图2,则折痕
,得到图2,则折痕![]() 的长为____________.
的长为____________.
【答案】![]()
【解析】
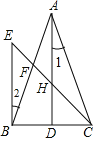
由折叠的性质可知△DFM为直角三角形,且DF=![]() AD=2,可证△ABE≌△
AD=2,可证△ABE≌△![]() DE,在Rt△ABE中,由勾股定理求BE,利用△ABE∽△FDM,可得对应边的比相等可求MF,继而求出MN的长.
DE,在Rt△ABE中,由勾股定理求BE,利用△ABE∽△FDM,可得对应边的比相等可求MF,继而求出MN的长.
解:如图,由已知可得MN垂直平分AD,DF=![]() AD=2,FN=
AD=2,FN=![]() AB=
AB=![]() ,
,
∵AB=CD=![]() D,∠A=∠
D,∠A=∠![]() =90°,∠AEB=∠
=90°,∠AEB=∠![]() ED,
ED,
∴△ABE≌△![]() DE,∴BE=ED, ∠ABE=∠
DE,∴BE=ED, ∠ABE=∠![]() DE
DE
设AE=x,则BE=ED=4-x,
在Rt△ABE中,由勾股定理得
AB2+AE2=BE2,即32+x2=(4-x)2,
解得x=![]() ,∴AE=
,∴AE=![]()
∵∠ABE=∠![]() DE, ∠BAE=∠
DE, ∠BAE=∠![]() =90°,
=90°,
∴△ABE∽△FDM,
∴![]() =
=![]() ,即
,即 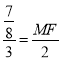 ,
,
解得MF=![]() .
.
∴MN=NF+FM=![]() +
+![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某校为改善办学条件,计划购进![]() 两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
A | 240 | 0 | 210 | 20 |
B | 300 | 0 | 250 | 30 |
(Ⅰ)如果在线下购买![]() 两种书架20个,共花费5520元,求
两种书架20个,共花费5520元,求![]() 两种书架各购买了多少个;
两种书架各购买了多少个;
(Ⅱ)如果在线上购买![]() 两种书架20个,共花费
两种书架20个,共花费![]() 元,设其中
元,设其中![]() 种书架购买
种书架购买![]() 个,求W关于
个,求W关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)在(Ⅱ)的条件下,若购买![]() 种书架的数量不少于
种书架的数量不少于![]() 种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.
种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.