题目内容
【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
俯角为α其中tanα=2![]() ,无人机的飞行高度AH为500
,无人机的飞行高度AH为500![]() 米,桥的长度为1255米.
米,桥的长度为1255米.
①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.
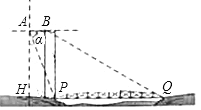
【答案】①求点H到桥左端点P的距离为250米;②无人机的长度AB为5米.
【解析】
试题分析:①在Rt△AHP中,由tan∠APH=tanα=![]() ,即可解决问题;②设BC⊥HQ于C.在Rt△BCQ中,求出CQ=
,即可解决问题;②设BC⊥HQ于C.在Rt△BCQ中,求出CQ=![]() =1500米,由PQ=1255米,可得CP=245米,再根据AB=HC=PH﹣PC计算即可;
=1500米,由PQ=1255米,可得CP=245米,再根据AB=HC=PH﹣PC计算即可;
试题解析:①在Rt△AHP中,∵AH=500![]() ,
,
由tan∠APH=tanα=![]() =2
=2![]() ,可得PH=250米.
,可得PH=250米.
∴点H到桥左端点P的距离为250米.
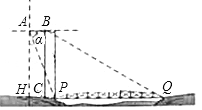
②设BC⊥HQ于C.
在Rt△BCQ中,∵BC=AH=500![]() ,∠BQC=30°,
,∠BQC=30°,
∴CQ=![]() =1500米,∵PQ=1255米,∴CP=245米,
=1500米,∵PQ=1255米,∴CP=245米,
∵HP=250米,∴AB=HC=250﹣245=5米.
答:这架无人机的长度AB为5米.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目