Question

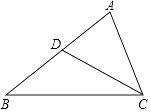
【题目】如图，在△ABC中，∠C=90°，AC=8，BC=6，D是边AB的中点，现有一点P位于边AC上，使得△ADP与△ABC相似，则线段AP的长为 ．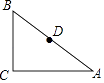

Answer 1

【答案】4或
【解析】解：∵在△ABC中，∠C=90°，AC=8，BC=6， ∴AB= =10．
∵D是边AB的中点，
∴AD=5．
当△ADP∽△ABC时， = ，即 = ，解得AP=4；
当△ADP∽△ACB时， = ，即 = ，解得AP= ．
所以答案是：4或 ．
【考点精析】通过灵活运用相似三角形的判定，掌握相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）即可以解答此题．