题目内容
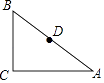
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6. 
(1)实践操作:尺规作图,不写作法,保留作图痕迹. ①作∠ABC的角平分线交AC于点D.
②作线段BD的垂直平分线,交AB于点E,交BC于点F,连接DE、DF.
(2)推理计算:四边形BFDE的面积为
【答案】
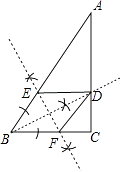
(1)解:如图,DE、DF为所作;
(2)8 ![]()
【解析】解:(2)∵∠C=90°,∠A=30°, ∴∠ABC=60°,AB=2BC=12,
∵BD为∠ABC的角平分线,
∴∠DBC=∠EBD=30°,
∵EF垂直平分BD,
∴FB=FD,EB=ED,
∴∠FDB=∠DBC=30°,∠EDB=∠EBD=30°,
∴DE∥BF,BE∥DF,
∴四边形BEDF为平行四边形,
而FB=FD,
∴四边形BEDF为菱形,
在Rt△ADE中,DE= ![]() AE,
AE,
而AE=AB﹣BE,
∴12﹣BE= ![]() BE,解得BE=8,
BE,解得BE=8,
在Rt△BDC中,CD= ![]() BC=2
BC=2 ![]() ,
,
∴四边形BFDE的面积= ![]() ×8×2
×8×2 ![]() =8
=8 ![]() .
.
所以答案是8 ![]() .
.
【考点精析】关于本题考查的线段垂直平分线的性质和含30度角的直角三角形,需要了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能得出正确答案.

 阅读快车系列答案
阅读快车系列答案【题目】某小学三年级到六年级的全体学生参加“礼仪”知识测试,试题共有10题,每题10分.从中随机抽取了部分学生的成绩进行统计,发现抽测的学生每人至少答对了6题,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”.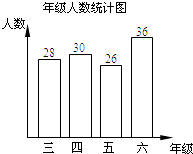
成绩情况统计表
成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 | 0.3 |
根据图表中提供的信息,回答下列问题:
(1)请将统计表补充完整
成绩情况统计表
成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 | 0.3 |
(2)测试学生中,成绩为80分的学生人数有 名;众数是 分;中位数是 分;
(3)若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有 名.