题目内容
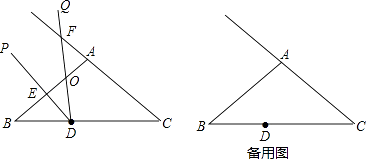
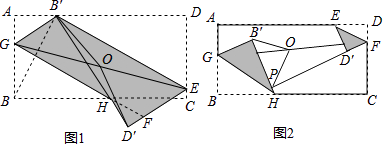
【题目】如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项. 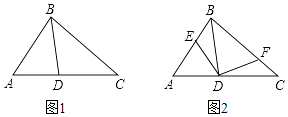
(1)求证:∠ACB=∠ABD;
(2)现有点E、F分别在边AB、BC上如图2,满足∠EDF=∠A+∠C,当AB=4,BC=5,CA=6时,求证:DE=DF.
【答案】
(1)证明:∵AB是AD与AC的比例中项.
∴ ![]() ,
,
又∵∠A=∠A,
∴△ABD∽△ACB,
∴∠ACB=∠ABD
(2)证明:∵△ABD∽△ACB,
∴ ![]() ,即
,即 ![]() ,
,
解得:AD= ![]() ,BD=
,BD= ![]() ,
,
∴CD=AC﹣AD=6﹣ ![]() =
= ![]() ,
,
∴BD=CD,
∴∠DBC=∠ACB,
∵∠ACB=∠ABD,
∴∠ABD=∠BDC,
∵∠EDF=∠A+∠C,∠A+∠C=180°﹣∠ABC,
∴∠EDF+∠ABC=180°,
∴点B、E、D、F四点共圆,
∴ ![]() ,
,
∴DE=DF
【解析】(1)证出△ABD∽△ACB,得出对应角相等即可;(2)由相似三角形的性质得出对应边成比例求出AD= ![]() ,BD=
,BD= ![]() ,得出BD=CD,由等腰三角形的性质得出∠DBC=∠ACB,证出∠ABD=∠BDC,再证明点B、E、D、F四点共圆,由圆周角定理得出
,得出BD=CD,由等腰三角形的性质得出∠DBC=∠ACB,证出∠ABD=∠BDC,再证明点B、E、D、F四点共圆,由圆周角定理得出 ![]() ,即可得出结论.
,即可得出结论.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

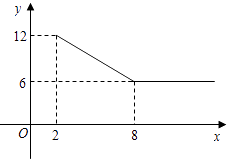
【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定: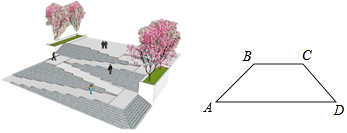
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.