题目内容
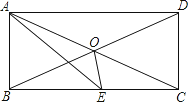
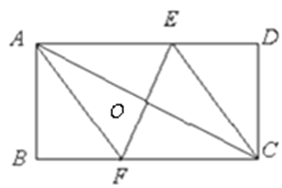
如图,矩形ABCD中, cm,
cm, cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.

(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且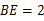 cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
 cm,
cm, cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且
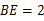 cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?(1)8秒 (2)第2秒或6秒时,点A、E、M、N组成平行四边形
分析:(1)相遇时,M点和N点所经过的路程和正好是矩形的周长,在速度已知的情况下,只需列方程即可解答.
(2)因为按照N的速度和所走的路程,在相遇时包括相遇前,N一直在AD上运动,当点M运动到BC边上的时候,点A、E、M、N才可能组成平行四边形,其中有两种情况,即当M到C点时以及在BC上时,所以要分情况讨论.
解:(1)设t秒时两点相遇,则有 ,解得
,解得 .
.
答:经过8秒两点相遇.
(2)由(1)知,点N一直在AD边上运动,所以当点M运动到BC边上的时候,点A、E、M、N才可能组成平行四边形,
设经过x秒,四点可组成平行四边形.分两种情形:
 ,解得
,解得 ;
;
② ,解得
,解得 .
.
答:第2秒或6秒时,点A、E、M、N组成平行四边形.
(2)因为按照N的速度和所走的路程,在相遇时包括相遇前,N一直在AD上运动,当点M运动到BC边上的时候,点A、E、M、N才可能组成平行四边形,其中有两种情况,即当M到C点时以及在BC上时,所以要分情况讨论.
解:(1)设t秒时两点相遇,则有
 ,解得
,解得 .
.答:经过8秒两点相遇.
(2)由(1)知,点N一直在AD边上运动,所以当点M运动到BC边上的时候,点A、E、M、N才可能组成平行四边形,
设经过x秒,四点可组成平行四边形.分两种情形:
 ,解得
,解得 ;
;②
 ,解得
,解得 .
.答:第2秒或6秒时,点A、E、M、N组成平行四边形.

练习册系列答案
相关题目
 处,当△
处,当△ 为直角三角形时,BE的长为
为直角三角形时,BE的长为 
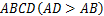 ,将纸片折叠一次,使点
,将纸片折叠一次,使点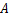 与
与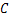 重合,再展开,折痕
重合,再展开,折痕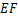 交
交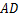 边于
边于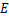 ,交
,交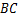 边于
边于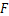 ,分别连接
,分别连接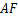 和
和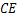 .
.
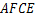 是菱形.
是菱形.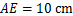 ,△
,△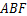 的面积为
的面积为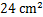 ,求△
,求△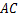 上是否存在一点
上是否存在一点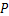 ,使得
,使得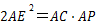 ?若存在,请说明点
?若存在,请说明点 中,
中, 6,
6, 8,
8, 平分∠
平分∠ 交
交 于点
于点 ,
,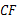 平分∠
平分∠ 交
交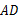 于点
于点 .
.
 为平行四边形;
为平行四边形;
 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)

 ,则AD的长为__________.
,则AD的长为__________.