题目内容
阅读下面材料:
小明遇到这样一个问题:如图1,在边长为 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)


请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 ,则AD的长为__________.
,则AD的长为__________.

小明遇到这样一个问题:如图1,在边长为
 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)

请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若
 ,则AD的长为__________.
,则AD的长为__________.
(1)这个新的正方形的边长为a;(2)正方形MNPQ的面积为2;(3)AD的长为 .
.
 .
.试题分析:(1)四个等腰直角三角形的斜边长为a,其拼成的正方形面积为a2,边长为a;
(2)如题图2所示,正方形MNPQ的面积等于四个虚线小等腰直角三角形的面积之和,据此求出正方形MNPQ的面积;
(3)参照小明的解题思路,对问题做同样的等积变换.如答图1所示,三个等腰三角形△RSF,△QET,△PDW的面积和等于等边三角形△ABC的面积,故阴影三角形△PQR的面积等于三个虚线等腰三角形的面积之和.据此列方程求出AD的长度.
试题解析:(1)四个等腰直角三角形的斜边长为a,则斜边上的高为
 a,
a,每个等腰直角三角形的面积为:
 a•
a• a=
a= a2,
a2,则拼成的新正方形面积为:4×
 a2=a2,即与原正方形ABCD面积相等,
a2=a2,即与原正方形ABCD面积相等,∴这个新正方形的边长为a;
(2)∵四个等腰直角三角形的面积和为a2,正方形ABCD的面积为a2,
∴S正方形MNPQ=S△ARE+S△DWH+S△GCT+S△SBF=4S△ARE=4×
 ×12=2;
×12=2;(3)如答图1所示,分别延长RD,QF,PE,交FA,EC,DB的延长线于点S,T,W.

由题意易得:△RSF,△QET,△PDW均为底角是30°的等腰三角形,其底边长均等于△ABC的边长.
不妨设等边三角形边长为a,则SF=AC=a.
如答图2所示,过点R作RM⊥SF于点M,则MF=
 SF=
SF= a,
a,
在Rt△RMF中,RM=MF•tan30°=
 a×
a× =
= a,
a,∴S△RSF=
 a•
a• a=
a= a2.
a2.过点A作AN⊥SD于点N,设AD=AS=x,
则AN=AD•sin30°=
 x,SD=2ND=2ADcos30°=
x,SD=2ND=2ADcos30°= x,
x,∴S△ADS=
 SD•AN=
SD•AN= •
• x•
x• x=
x= x2.
x2.∵三个等腰三角形△RSF,△QET,△PDW的面积和=3S△RSF=3×
 a2=
a2= a2,
a2,∴S△RPQ=S△ADS+S△CFT+S△BEW=3S△ADS,
∴
 =3×
=3× x2,得x2=
x2,得x2=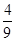 ,
,解得x=
 或x=
或x= (不合题意,舍去)
(不合题意,舍去)∴x=
 ,即AD的长为
,即AD的长为 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 cm,
cm, cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
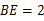 cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形? 中,对角线
中,对角线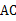 、
、 相交于点O,E为BC的中点,则下列式子中,一定成立的是( )
相交于点O,E为BC的中点,则下列式子中,一定成立的是( )




