题目内容
已知矩形 中,
中, 6,
6, 8,
8, 平分∠
平分∠ 交
交 于点
于点 ,
,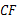 平分∠
平分∠ 交
交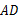 于点
于点 .
.

(1)说明四边形 为平行四边形;
为平行四边形;
(2)求四边形 的面积.
的面积.
 中,
中, 6,
6, 8,
8, 平分∠
平分∠ 交
交 于点
于点 ,
,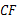 平分∠
平分∠ 交
交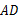 于点
于点 .
.
(1)说明四边形
 为平行四边形;
为平行四边形;(2)求四边形
 的面积.
的面积.(1)见解析 (2)30
分析:(1)可证明 ∥
∥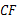 ,又
,又 ∥
∥ ,可证四边形
,可证四边形 为平行四边形.
为平行四边形.
(2)先求△ 的面积,再求平行四边形
的面积,再求平行四边形 的面积.
的面积.
解:(1)∵ 四边形 是矩形,
是矩形,
∴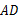 ∥
∥ ,
, ∥
∥ ,∴
,∴ 
∵ 平分
平分 ,
,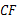 平分
平分 ,
,
∴ .∴
.∴  ∥
∥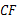 .
.
∴ 四边形 为平行四边形(两组对边分别平行的四边形是平行四边形).
为平行四边形(两组对边分别平行的四边形是平行四边形).
(2)如图,作 ⊥
⊥ 于点
于点 .
.

∵ 平分∠
平分∠ ,∴
,∴  (角平分线的性质).
(角平分线的性质).
又 ,
,
∴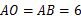 ,
, .
.
在Rt△ 中,设
中,设 ,则
,则 ,
,
那么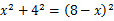 ,解得
,解得 .
.
∴ 平行四边形 的面积等于
的面积等于 .
.
 ∥
∥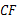 ,又
,又 ∥
∥ ,可证四边形
,可证四边形 为平行四边形.
为平行四边形.(2)先求△
 的面积,再求平行四边形
的面积,再求平行四边形 的面积.
的面积.解:(1)∵ 四边形
 是矩形,
是矩形,∴
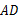 ∥
∥ ,
, ∥
∥ ,∴
,∴ 
∵
 平分
平分 ,
,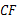 平分
平分 ,
,∴
 .∴
.∴  ∥
∥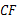 .
.∴ 四边形
 为平行四边形(两组对边分别平行的四边形是平行四边形).
为平行四边形(两组对边分别平行的四边形是平行四边形).(2)如图,作
 ⊥
⊥ 于点
于点 .
.
∵
 平分∠
平分∠ ,∴
,∴  (角平分线的性质).
(角平分线的性质).又
 ,
,∴
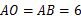 ,
, .
.在Rt△
 中,设
中,设 ,则
,则 ,
,那么
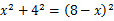 ,解得
,解得 .
.∴ 平行四边形
 的面积等于
的面积等于 .
.
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目

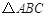 中,
中, ,
, 的垂直平分线
的垂直平分线 交
交 ,交
,交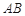 于点
于点 ,点
,点 在
在 .
.
 是平行四边形.
是平行四边形. 满足什么条件时,四边形
满足什么条件时,四边形
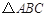 中,
中,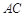 的垂直平分线分别交
的垂直平分线分别交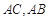 于点
于点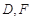 ,
, 交
交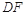 的延长线于点
的延长线于点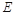 ,已知
,已知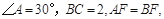 则四边形
则四边形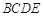 的面积是( )
的面积是( )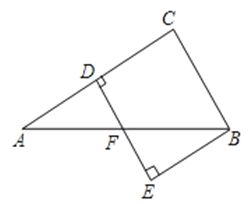

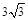

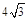
 的周长为
的周长为 ,两条对角线相交于点
,两条对角线相交于点 ,且△
,且△ 的周长比△
的周长比△ 的周长大
的周长大 ,则
,则 的长为( )
的长为( )



 cm,
cm, cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
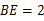 cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?