题目内容
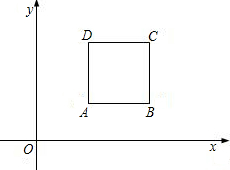
如图,四边形ABCD是正方形,已知A(5,4),B(10,4):
(1)求点C、D的坐标;
(2)若一次函数y=kx+3(k≠0)的图象过C点,求k的值;
(3)在(2)的条件下,①若将直线l:y=kx+3向下平移a个单位,将正方形分为上下两部分的面积比为7:3,试求出a的值;②若将直线l:y=kx+3平移后与以A为圆心,AC为半径的圆相切,直接写出平移后的直线的解析式.
(1)求点C、D的坐标;
(2)若一次函数y=kx+3(k≠0)的图象过C点,求k的值;
(3)在(2)的条件下,①若将直线l:y=kx+3向下平移a个单位,将正方形分为上下两部分的面积比为7:3,试求出a的值;②若将直线l:y=kx+3平移后与以A为圆心,AC为半径的圆相切,直接写出平移后的直线的解析式.

(1)已知A(5,4),B(10,4),则AB=5,即正方形的边长为5;
故C(10,9),D(5,9).
(2)将点C(10,9)代入直线l的解析式中,
得:10k+3=9,
即k=
.
(3)①设平移后的直线l′:y=
x+3-a(a>0);
1)当直线l′与线段AD、BC相交时,
设交点分别为M、N,则M(5,6-a),N(10,9-a);
故MA=2-a,NB=5-a;
由题意得:S梯形MABN=
(2-a+5-a)×5=25×
,
解得a=2;
2)当直线l′与线段AB、BC相交时,同1)可求得a=2;
综上可知:a=2.
②设平移后的直线l″:y=
x+3+b,即
x-y+3+b=0;
易知AC=5
,A(5,4);
由题意得:
=5
;
解得b=±2
-2;
故平移后的直线解析式为:y=
x+1-2
或y=
x+1+2
.
故C(10,9),D(5,9).
(2)将点C(10,9)代入直线l的解析式中,
得:10k+3=9,
即k=
| 3 |
| 5 |
(3)①设平移后的直线l′:y=
| 3 |
| 5 |
1)当直线l′与线段AD、BC相交时,
设交点分别为M、N,则M(5,6-a),N(10,9-a);
故MA=2-a,NB=5-a;
由题意得:S梯形MABN=
| 1 |
| 2 |
| 3 |
| 10 |
解得a=2;
2)当直线l′与线段AB、BC相交时,同1)可求得a=2;
综上可知:a=2.
②设平移后的直线l″:y=
| 3 |
| 5 |
| 3 |
| 5 |
易知AC=5
| 2 |
由题意得:
|
| ||||
|
| 2 |
解得b=±2
| 17 |
故平移后的直线解析式为:y=
| 3 |
| 5 |
| 17 |
| 3 |
| 5 |
| 17 |

练习册系列答案
相关题目