题目内容
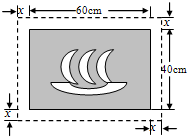
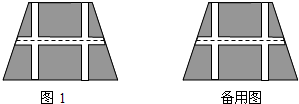
某工厂准备翻建新的厂门,厂门要求设计成轴对称的拱型曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的特种运输卡车的高度是3m,宽度是5.8m.现设计了两种方案:方案一:建成抛物线形状;方案二:建成圆弧形状(如图).为确保工厂的特种卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.
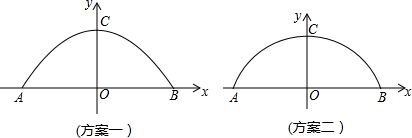
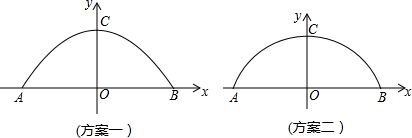
(1)第一方案:设抛物线的表达式是y=a(x+6)(x-6)
因C(0,4)在抛物线的图象上,代入表达式,
得a=-
.
故抛物线的表达式是y=-
x2+4.
把第一象限的点(t,3)代入函数
得3=-
t2+4
∴t=3
∴当高度是3m时,最大宽度是6m.
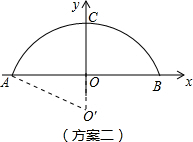 (2)第二方案:由垂径定理得:圆心O′在y轴上(原点的下方)
(2)第二方案:由垂径定理得:圆心O′在y轴上(原点的下方)
设圆的半径是R,那么在RT△OAO′中,由的勾股定理得:62+(R-4)2=R2
解得R=6.5
当高度是3m时,最大宽度=2
=4
≈6.9m
根据上面的计算得:为了工厂的特种卡车通过厂门更安全,所以采用第二种方案更合理.
因C(0,4)在抛物线的图象上,代入表达式,
得a=-
| 1 |
| 9 |
故抛物线的表达式是y=-
| 1 |
| 9 |
把第一象限的点(t,3)代入函数
得3=-
| 1 |
| 9 |
∴t=3
∴当高度是3m时,最大宽度是6m.
 (2)第二方案:由垂径定理得:圆心O′在y轴上(原点的下方)
(2)第二方案:由垂径定理得:圆心O′在y轴上(原点的下方)设圆的半径是R,那么在RT△OAO′中,由的勾股定理得:62+(R-4)2=R2
解得R=6.5
当高度是3m时,最大宽度=2
| R2-5.52 |
| 3 |
根据上面的计算得:为了工厂的特种卡车通过厂门更安全,所以采用第二种方案更合理.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
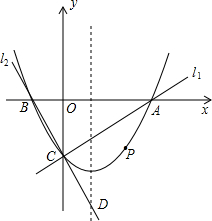
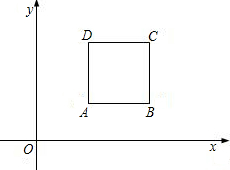
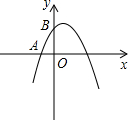
 (x,y)为整点,该函数的图象为整点抛物线(例如:y=x2+2x+2).
(x,y)为整点,该函数的图象为整点抛物线(例如:y=x2+2x+2).