题目内容
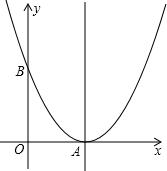
如图,以A为顶点的抛物线与y轴交于点B、已知A、B两点的坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设M(m,n)是抛物线上的一点(m、n为正整数),且它位于对称轴的右侧.若以M、B、O、A为顶点的四边形四条边的长度是四个连续的正整数,求点M的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点P,PA2+PB2+PM2>28是否总成立?请说明理由.
(1)求抛物线的解析式;
(2)设M(m,n)是抛物线上的一点(m、n为正整数),且它位于对称轴的右侧.若以M、B、O、A为顶点的四边形四条边的长度是四个连续的正整数,求点M的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点P,PA2+PB2+PM2>28是否总成立?请说明理由.

(1)设y=a(x-3)2,
把B(0,4)代入,
得a=
,
∴y=
(x-3)2;
(2)解法一:
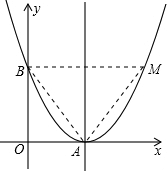 ∵四边形OAMB的四边长是四个连续的正整数,其中有3、4,
∵四边形OAMB的四边长是四个连续的正整数,其中有3、4,
∴可能的情况有三种:1、2、3、4;2、3、4、5;3、4、5、6,
∵M点位于对称轴右侧,且m,n为正整数,
∴m是大于或等于4的正整数,
∴MB≥4,
∵AO=3,OB=4,
∴MB只有两种可能,∴MB=5或MB=6,
当m=4时,n=
(4-3)2=
(不是整数,舍去);
当m=5时,n=
(不是整数,舍去);
当m=6时,n=4,MB=6;
当m≥7时,MB>6;
因此,只有一种可能,即当点M的坐标为(6,4)时,MB=6,MA=5,
四边形OAMB的四条边长分别为3、4、5、6.
解法二:
∵m,n为正整数,n=
(m-3)2,
∴(m-3)2应该是9的倍数,
∴m是3的倍数,
又∵m>3,
∴m=6,9,12,
当m=6时,n=4,
此时,MA=5,MB=6,
∴当m≥9时,MB>6,
∴四边形OAMB的四边长不能是四个连续的正整数,
∴点M的坐标只有一种可能(6,4).
(3)设P(3,t),MB与对称轴交点为D,
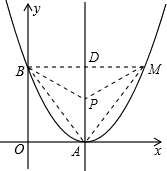 则PA=|t|,PD=|4-t|,PM2=PB2=(4-t)2+9,
则PA=|t|,PD=|4-t|,PM2=PB2=(4-t)2+9,
∴PA2+PB2+PM2=t2+2[(4-t)2+9]
=3t2-16t+50
=3(t-
)2+
,
∴当t=
时,PA2+PB2+PM2有最小值
;
∴PA2+PB2+PM2>28总是成立.
把B(0,4)代入,
得a=
| 4 |
| 9 |
∴y=
| 4 |
| 9 |
(2)解法一:
 ∵四边形OAMB的四边长是四个连续的正整数,其中有3、4,
∵四边形OAMB的四边长是四个连续的正整数,其中有3、4,∴可能的情况有三种:1、2、3、4;2、3、4、5;3、4、5、6,
∵M点位于对称轴右侧,且m,n为正整数,
∴m是大于或等于4的正整数,
∴MB≥4,
∵AO=3,OB=4,
∴MB只有两种可能,∴MB=5或MB=6,
当m=4时,n=
| 4 |
| 9 |
| 4 |
| 9 |
当m=5时,n=
| 16 |
| 9 |
当m=6时,n=4,MB=6;
当m≥7时,MB>6;
因此,只有一种可能,即当点M的坐标为(6,4)时,MB=6,MA=5,
四边形OAMB的四条边长分别为3、4、5、6.
解法二:
∵m,n为正整数,n=
| 4 |
| 9 |
∴(m-3)2应该是9的倍数,
∴m是3的倍数,
又∵m>3,
∴m=6,9,12,
当m=6时,n=4,
此时,MA=5,MB=6,
∴当m≥9时,MB>6,
∴四边形OAMB的四边长不能是四个连续的正整数,
∴点M的坐标只有一种可能(6,4).
(3)设P(3,t),MB与对称轴交点为D,
 则PA=|t|,PD=|4-t|,PM2=PB2=(4-t)2+9,
则PA=|t|,PD=|4-t|,PM2=PB2=(4-t)2+9,∴PA2+PB2+PM2=t2+2[(4-t)2+9]
=3t2-16t+50
=3(t-
| 8 |
| 3 |
| 86 |
| 3 |
∴当t=
| 8 |
| 3 |
| 86 |
| 3 |
∴PA2+PB2+PM2>28总是成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上部分点的横坐标与对应的纵坐标如下表:
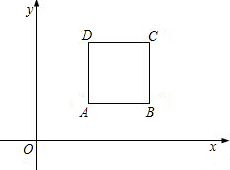
上部分点的横坐标与对应的纵坐标如下表: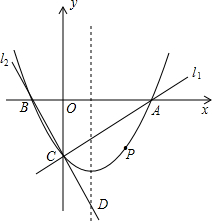

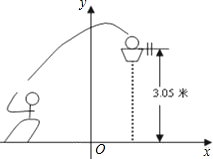 框内.已知篮框的中心离地面的距离为3.05米.
框内.已知篮框的中心离地面的距离为3.05米.