题目内容
两个直角边为6的全等的等腰直角三角形Rt△AOB和Rt△CED,按如图一所示的位置放置,点O与E重合.
(1)Rt△AOB固定不动,Rt△CED沿x轴以每秒2个单位长度的速度向右运动,当点E运动到与点B重合时停止,设运动x秒后,Rt△AOB和Rt△CED的重叠部分面积为y,求y与x之间的函数关系式;
(2)当Rt△CED以(1)中的速度和方向运动,运动时间x=2秒时,Rt△CED运动到如图二所示的位置,若抛物线y=
x2+bx+c过点A,G,求抛物线的解析式;
(3)现有一动点P在(2)中的抛物线上运动,试问点P在运动过程中是否存在点P到x轴或y轴的距离为2的情况?若存在,请求出点P的坐标;若不存在,请说明理由.
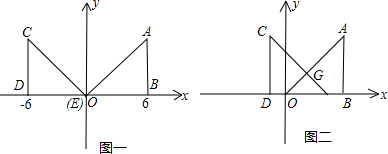
(1)Rt△AOB固定不动,Rt△CED沿x轴以每秒2个单位长度的速度向右运动,当点E运动到与点B重合时停止,设运动x秒后,Rt△AOB和Rt△CED的重叠部分面积为y,求y与x之间的函数关系式;
(2)当Rt△CED以(1)中的速度和方向运动,运动时间x=2秒时,Rt△CED运动到如图二所示的位置,若抛物线y=
| 1 |
| 4 |
(3)现有一动点P在(2)中的抛物线上运动,试问点P在运动过程中是否存在点P到x轴或y轴的距离为2的情况?若存在,请求出点P的坐标;若不存在,请说明理由.
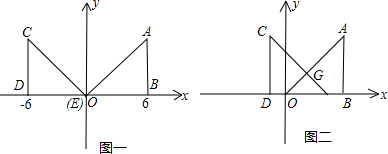
(1)①由题意知重叠部分是等腰直角三角形,作GH⊥OE.
∴OE=2x,GH=x,
∵y=
OE•GH=
•2x•x=x2(0≤x≤3)
(2)A(6,6)
当x=2时,OE=2×2=4.
∴OH=2,HG=2,
∴G(2,2).
∴X
∴y=
x2-x+3.
(3)设P(m,n).
当点P到y轴的距离为2时,
有|m|=2,
∴|m|=2.当m=2时,得n=2,
当m=-2时,得n=6.
当点P到x轴的距离为2时,有|n|=2.
∵y=
x2-x+3
=
(x-2)2+2>0
∴n=2.当n=2时,得m=2.
综上所述,符合条件的点P有两个,分别是P1(2,2),P2(-2,6).
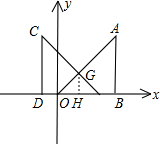
∴OE=2x,GH=x,
∵y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)A(6,6)
当x=2时,OE=2×2=4.
∴OH=2,HG=2,
∴G(2,2).
|
∴X
|
∴y=
| 1 |
| 4 |
(3)设P(m,n).
当点P到y轴的距离为2时,
有|m|=2,
∴|m|=2.当m=2时,得n=2,
当m=-2时,得n=6.
当点P到x轴的距离为2时,有|n|=2.
∵y=
| 1 |
| 4 |
=
| 1 |
| 4 |
∴n=2.当n=2时,得m=2.
综上所述,符合条件的点P有两个,分别是P1(2,2),P2(-2,6).


练习册系列答案
相关题目
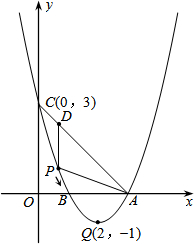
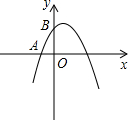
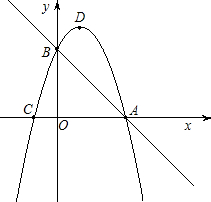 物线与x轴的另一个交点为C,抛物线的顶点为D.
物线与x轴的另一个交点为C,抛物线的顶点为D.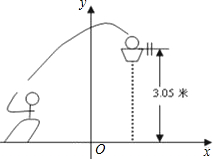 框内.已知篮框的中心离地面的距离为3.05米.
框内.已知篮框的中心离地面的距离为3.05米.
 各安装一盏路灯,两灯间的水平距离CD=8米,
各安装一盏路灯,两灯间的水平距离CD=8米, 鸡场,设它的长度为xm.
鸡场,设它的长度为xm.