题目内容
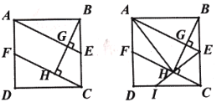
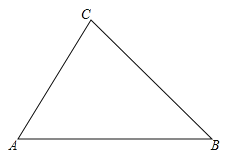
【题目】如图,已知△ABC,请用直尺(不带刻度),和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).
(1)作菱形AMNP,使点M,N、P在边AB、BC、CA上;
(2)当∠A=60°,AB=8,AC=6时,求菱形AMNP的面积.
【答案】(1)详见解析;(2)![]()
【解析】
(1)作∠BAC的角平分线交BC于N,作线段AN的垂直平分线交AC于点P,交AB于点M,连接MN,PN,四边形AMNP是菱形.
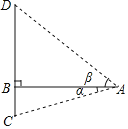
(2)如图,作CF⊥AN于F,BE⊥AN于E.想办法求出AN,PM即可.
解:(1)菱形AMNP如图所示.
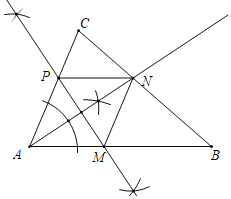
(2)如图,作CF⊥AN于F,BE⊥AN于E.

在Rt△ACF中,![]() 菱形
菱形![]() ,
,
![]() ∠CAF=
∠CAF=![]() 30°,
30°,
∵∠AFC=90°,AC=6,
∴CF=3,![]()
同法可得:BE=4,![]()
∴EF=AE-AF=![]() ,
,
∵CF∥BE,
∴![]()
∴EN=![]() EF=
EF= ![]()
∴AN=AE-EN=![]()
![]() 菱形
菱形![]() ,
,
![]() 且
且![]() 与
与![]() 互相平分,
互相平分,
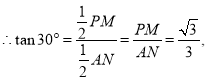
![]()
∴S菱形AMNP= ![]()

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案【题目】九年级某班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会.抽奖方案如下:将一副扑克牌中点数为“2”、“3”、“3”、“5”、“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖.记每次抽出两张牌点数之差为![]() ,按下表要求确定奖项.
,按下表要求确定奖项.
奖项 | 一等奖 | 二等奖 | 三等奖 |
|
|
|
|
(1)用列表法或画树状图的方法求出甲同学获二等奖的概率;
(2)判断是否每次抽奖都会获奖?请说明理由.
【题目】某校为了解八年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知![]() .
.![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图中相关数据回答下列问题:
,请结合图中相关数据回答下列问题:
发言次数 | |
|
|
|
|
|
|
|
|
|
|
|
|
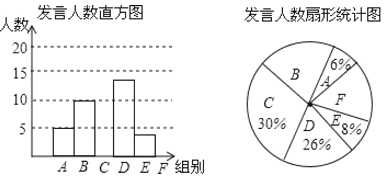
(1)求出样本容量,并补全直方图;
(2)该年级共有学生1500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知![]() 组发言的学生中恰有1位男生,
组发言的学生中恰有1位男生,![]() 组发言的学生中有2位女生.现从
组发言的学生中有2位女生.现从![]() 组与
组与![]() 组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率
组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率