题目内容
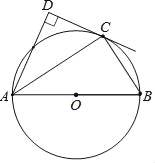
【题目】如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长.
【答案】(1)证明见解析;(2)AE=3![]() .
.
【解析】分析: (1)要证EF是⊙O的切线,只要连接OE,再证∠FEO=90°即可;
(2)证明△FEA∽△FBA,得出AE,BF的比例关系式,勾股定理得出AE,BF的关系式,求出AE的长.
详解:
(1)证明:连接OE,
∵∠B的平分线BE交AC于D,
∴∠CBE=∠ABE.
∵EF∥AC,
∴∠CAE=∠FEA.
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB.
∵∠AEB=90°,
∴∠FEO=90°.
∴EF是⊙O切线.
(2)解:∵AFFB=EFEF,
∴AF×(AF+15)=10×10.
∴AF=5.
∴FB=20.
∵∠F=∠F,∠FEA=∠FBE,
∴△FEA∽△FBE.
∴EF=10
∵AE2+BE2=15×15.
∴AE=3![]() .
.

点睛: 本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
【题目】某路公交车从起点出发,经过A、B、C三站到达终点,途中上下乘客如下表所示.(正数表示上车的人数,负数表示下车的人数)
上(下)车 | 起点 | A | B | C | 终点 |
上车的人数 | 10 | 9 | 6 | 5 | 0 |
下车的人数 | 0 | ﹣2 | ﹣5 | ﹣6 | ? |
(1)表格中“?”应填 .
(2)车行驶在哪两站之间时,车上的乘客最多? 站和 站;
(3)若每人乘坐一站需要买票1元,则该车出车一次能收入多少钱?要求写出计算过程.