Question

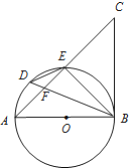
【题目】 如图，在Rt△ABC中，∠C=90°，点O在边BC上，以点O为圆心，OB为半径的圆经过点A，过点A作直线AD，使∠CAD=2∠B．

（1）判断直线AD与⊙O的位置关系，并说明理由；

（2）若OB=4，∠CAD=60°，请直接写出图中弦AB与围成的阴影部分的面积．

Answer 1

【答案】（1）直线AD与⊙O的位置关系是相切，理由见解析；（2）-4

【解析】

（1）连接OA，根据等腰三角形的性质得到∠OAB=∠B，求得∠CAD=∠COA，推出OA⊥AD，于是得到结论；

（2）根据邻补角的定义得到∠AOB=120°，根据扇形和三角形的面积公式即可得到结论．

解：（1）直线AD与⊙O的位置关系是相切，

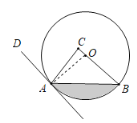
理由：连接OA，

∵OA=OB，

∴∠OAB=∠B，

∴∠COA=2∠B，

∵∠CAD=2∠B，

∴∠CAD=∠COA，

∵∠C=90°，

∴∠COA+∠OAC=90°，

∴∠CAO＋∠CAD=90°，

∴∠OAD=90°，

∴OA⊥AD，

∴直线AD与⊙O相切；

（2）∵∠CAD=60°，

∴∠COA=∠CAD=60°，

∴∠AOB=120°，

∴∠B=∠OAB=30°，

∵OB=4

∴OA=OB=4

在Rt△OAC中，AC=OA·sin∠COA=2

∴阴影部分的面积=S扇形AOB-S△AOB=-OB·AC=-4．