题目内容
【题目】九年级某班组织班级联欢会，最后进入抽奖环节，每名同学都有一次抽奖机会．抽奖方案如下：将一副扑克牌中点数为“2”、“3”、“3”、“5”、“6”的五张牌背面朝上洗匀，先从中抽出1张牌，再从余下的4张牌中抽出1张牌，记录两张牌点数后放回，完成一次抽奖．记每次抽出两张牌点数之差为
，按下表要求确定奖项．
奖项 | 一等奖 | 二等奖 | 三等奖 |
|
|
|
|
（1）用列表法或画树状图的方法求出甲同学获二等奖的概率；
（2）判断是否每次抽奖都会获奖？请说明理由．
【答案】（1）树状图见解析，
(甲获二等奖)
；（2）不一定，当两张牌都抽到3时，
，则他不会获奖．
【解析】
（1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与甲同学获得二等奖的情况，再利用概率公式即可求得答案；
（2）由树状图可得：当两张牌都是3时，，不会有奖．
解：（1）画树状图得：
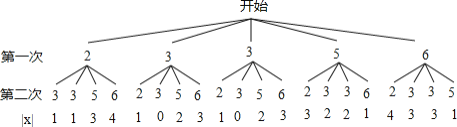
共有20种等可能的结果，甲同学获得二等奖的有6种情况，
甲同学获得二等奖的概率为：
；
（2）由（1）可知，当两张牌都是3时，，不会有奖．
练习册系列答案
相关题目
