Question

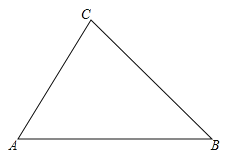
【题目】如图1，正方形ABCD中，点E是BC的中点，过点B作BG⊥AE于点G，过点C作CF垂直BG的延长线于点H，交AD于点F

(1)求证：△ABG≌△BCH；

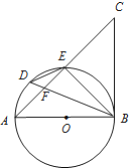
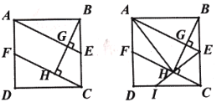
(2)如图2，连接AH，连接EH并延长交CD于点I；

求证：① AB2=AE·BH；② 求的值；

Answer 1

【答案】（1）见解析；（2）①见解析；②

【解析】

（1）根据正方形的性质证得AB=BC，∠ABC=90°，根据垂直得到∠AGB=∠BHC=90°，再证明∠GAB=∠CBH即可得到结论；

（2）①根据两组角分别相等证明△ABE∽△BHC即可得到结论；

②证明四边形AECF是平行四边形得到AF=CE=,证明AH=AB，得到AH=2AF，证明△AFH∽△IHC得到,连接AI，证明△AHI≌△ADI，得到=.

（1）∵四边形ABCD是正方形，

∴AB=BC，∠ABC=90°，

∴∠ABG+∠CBH=90°，

∵BG⊥AE，BH⊥CF，

∴∠AGB=∠BHC=90°，

∴∠GAB+∠ABG=90°，

∴∠GAB=∠CBH,

∴△ABG≌△BCH；

（2）①∵∠EAB=∠CBH，∠ABE=∠BHC=90°，

∴△ABE∽△BHC,

∴，

∵AB=BC，

∴AB2=AE·BH；

②∵AE⊥BH,CF⊥BH,

∴AE∥CF，

∵AF∥CE,

∴四边形AECF是平行四边形，

∴AF=CE=,

∵EH==BE，AE⊥BH，

∴BG=GH，

∴AE垂直平分BH，

∴AH=AB=BC=2AF，

∴∠AHB=∠ABH=∠BCH，

∴∠AHF=∠HCI,

∵∠BAE=∠CBH，∠BAH=2∠BAE，∠CEI=2∠CBH，

∴∠BAH=∠CEI，

∴∠AFH=∠CIH，

∴△AFH∽△IHC，

∴,

连接AI，

∵∠ABH=∠AHB，∠EBH=∠EHB,

∴∠AHE=∠ABE=90°，

∴∠AHI=90°=∠D,

∵AH=AB=AD，AI=AI，

∴△AHI≌△ADI,

∴DI=HI,

∴=.