题目内容
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交与A(4,-2),B(-2,n)两点,与
的图像交与A(4,-2),B(-2,n)两点,与![]() 轴交与点C.
轴交与点C.
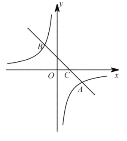
(1)求![]() ,n的值;
,n的值;
(2)请直接写出不等式![]() 的解集;
的解集;
(3)点A关于![]() 轴对称得到点A’,连接A’B,A’C,求△A’BC的面积.
轴对称得到点A’,连接A’B,A’C,求△A’BC的面积.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)8.
;(3)8.
【解析】
(1)将A点坐标代入![]() 即可求得
即可求得![]() 的值,再根据求得的解析式即可求得n的值;
的值,再根据求得的解析式即可求得n的值;
(2)用函数的观察,反比例函数图象在一次函数图象上面部分的x取值范围,即为不等式的解集;
(3)求出对称点坐标,再根据![]() 即可求得面积.
即可求得面积.
解:(1)将A(4,-2)代入![]() ,得k2=-8,
,得k2=-8,
∴![]() ,
,
将(-2,n)代入![]() 得n=4,
得n=4,
∴k2=-8,n=4;
(2)根据函数图象可知![]() 的解集为:-2<x<0或x>4;
的解集为:-2<x<0或x>4;
(3)将A(4,-2),B(-2,4)代入y=k1x+b,得k1=-1,b=2
∴一次函数的关系式为y=-x+2,
与x轴交于点C(2,0),
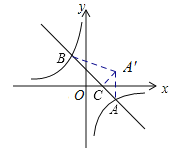
∴图象沿x轴翻折后,得A′(4,2),
![]() .
.
∴△A'BC的面积为8.

练习册系列答案
相关题目
【题目】我市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为![]() .
.
(1)根据题意,填写下表:
单人间的房间数 | 10 | … |
| … | 30 |
双人间的房间数 | _________ | … |
| … | 60 |
三人间的房间数 | 70 | … | _________ | … | _________ |
养老床位数 | 260 | … | _________ | … | _________ |
(2)若该养老中心建成后可提供养老床位200个,求![]() 的值;
的值;
(3)求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?