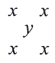Question

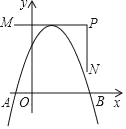
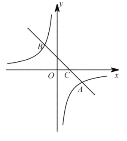
【题目】抛物线y＝ax2+bx﹣5的图象与x轴交于A、B两点，与y轴交于点C，其中点A坐标为(﹣1，0)，一次函数y＝x+k的图象经过点B、C．

（1）试求二次函数及一次函数的解析式；

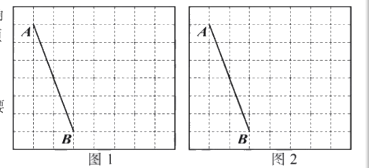
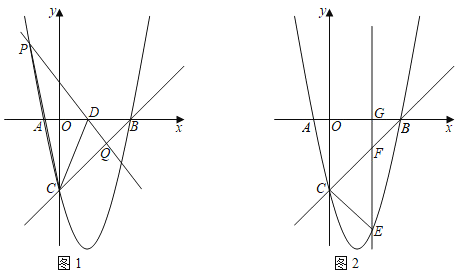
（2）如图1，点D(2，0)为x轴上一点，P为抛物线上的动点，过点P、D作直线PD交线段CB于点Q，连接PC、DC，若S△CPD＝3S△CQD，求点P的坐标；

（3）如图2，点E为抛物线位于直线BC下方图象上的一个动点，过点E作直线EG⊥x轴于点G，交直线BC于点F，当EF+CF的值最大时，求点E的坐标．

Answer 1

【答案】（1）y＝x2﹣4x﹣5，y＝x﹣5；（2）(，)或(，)或(2，﹣9)或(3，﹣8)；（3）E(3，﹣8)

【解析】

（1）首先确定点C的坐标，代入一次函数求出k，可得点B的坐标，设抛物线的解析式为y＝a（x+1）（x﹣5）＝ax2﹣4ax﹣5a，构建方程求出a即可解决问题．

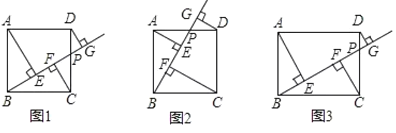
（2）分两种情形：①当点P在直线BC的上方时，如图2﹣1中，作DH∥BC交y轴于H，过点D作直线DT交y轴于T，交BC于K，作PT∥BC交抛物线于P，直线PD交抛物线于Q．②当点P在直线BC的下方时，如图2﹣2中，分别求解即可解决问题．

（3）设E（m，m2﹣4m﹣5），则F（m，m﹣5），构建二次函数，利用二次函数的性质解决问题即可．

解：（1）∵抛物线y＝ax2+bx﹣5的图象与y轴交于点C，

∴C（0，﹣5），

∵一次函数y＝x+k的图象经过点B、C，

∴k＝﹣5，

∴B（5，0），

设抛物线的解析式为y＝a（x+1）（x﹣5）＝ax2﹣4ax﹣5a，

∴﹣5a＝﹣5，

∴a＝1，

∴二次函数的解析式为y＝x2﹣4x﹣5，一次函数的解析式为y＝x﹣5．

（2）①当点P在直线BC的上方时，如图2﹣1中，作DH∥BC交y轴于H，过点D作直线DT交y轴于T，交BC于K，作PT∥BC交抛物线于P，直线PD交抛物线于Q．

∵S△CPD＝3S△CQD，

∴PD＝3DQ，

∵PT∥DH∥BC，

∴，

∵D（2，0），B（5，0），C（﹣5，0），

∴OA＝OB＝5，OD＝OH＝2，

∴HC＝3，

∴TH＝9，OT＝7，

∴直线PT的解析式为y＝x+7，

由，解得或，

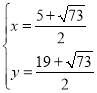∴P（，）或（，），

②当点P在直线BC的下方时，如图2﹣2中，

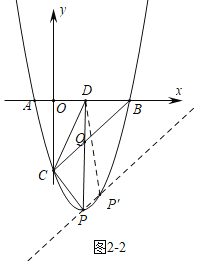
当点P与抛物线的顶点（2，﹣9）重合时，PD＝9．DQ＝3，

∴PQ＝3DQ，

∴S△CPD＝3S△CQD，

过点P作PP′∥BC，此时点P′也满足条件，

∵直线PP′的解析式为y＝x﹣11，

由，解得或，

∴P′（2，﹣9），P′（3，﹣8），

综上所述，满足条件的点P的坐标为（，）

或（，）或（2，﹣9）或（3，﹣8）．

（3）设E（m，m2﹣4m﹣5），则F（m，m﹣5），

∴EF＝（m﹣5）﹣（m2﹣4m﹣5）＝5m﹣m2，CF＝m，

∴EF+CF＝﹣m2+6m＝﹣（m﹣3）2+9，

∵﹣1＜0，

∴m＝3时，EF+CF的值最大，此时E（3，﹣8）．