题目内容
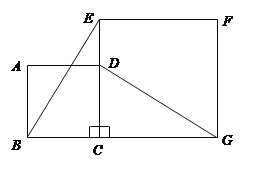
【题目】如图,直角梯形![]() 中,
中,![]() 的圆心
的圆心![]() 从点
从点![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度向点
的速度向点![]() 运动,
运动,![]() 的圆心
的圆心![]() 从点
从点![]() 开始沿
开始沿![]() 边以
边以![]()
![]() 的速度向点
的速度向点![]() 运动,
运动,![]() 半径为
半径为![]() 的半径为
的半径为![]() ,若
,若![]() 分别从点
分别从点![]() 、点
、点![]() 同时出发,运动的时间为
同时出发,运动的时间为![]()
(1)请求出![]() 与腰
与腰![]() 相切时
相切时![]() 的值;
的值;
(2)在![]() 范围内,当
范围内,当![]() 为何值时,
为何值时,![]() 与
与![]() 外切?
外切?
【答案】(1)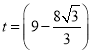 ;(2)3
;(2)3
【解析】
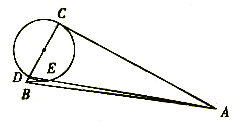
(1)先设⊙O2运动到E与CD相切,且切点是F;连接EF,并过E作EG∥BC,交CD于G,再过G作GH⊥BC于H,那么就得到直角三角形EFG和矩形GEBH.要求⊙O2与CD相切的时间,可以先求出⊙O2从B到E所走的路程BE,即GH的长,再除以运动速度即可.那么求GH的值就是关键,由∠C=60°,可以知道∠CGH=30°,那么∠FGE=60°.在Rt△EFG中,可以利用勾股定理求出EG的值,那么CH=BCBH=BCEG.在Rt△CGH中,利用60°的角的正切值可求出GH的值,此问就可解了;
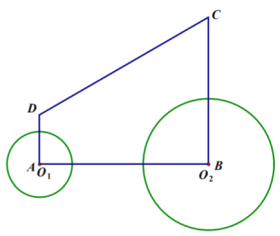
(2)因为![]() ,所以O1一定在AD上,连接O1O2.利用勾股定理可得到关于t的一元二次方程,求解即可,根据要求,可选择t的值.
,所以O1一定在AD上,连接O1O2.利用勾股定理可得到关于t的一元二次方程,求解即可,根据要求,可选择t的值.
解:![]() 如图所示,设点
如图所示,设点![]() 运动到点
运动到点![]() 处时,
处时,![]() 与腰
与腰![]() 相切
相切
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]()
作![]() ,交
,交![]() 于
于![]() ,作
,作![]() ,垂足为
,垂足为![]()
由直角三角形GEF中,∠EGF+∠GEF=90°,
又∠EGF+∠CGH=90°,
∴∠GEF=∠CGH=30°,
设FG=xcm,则EG=2xcm,又EF=4cm,
根据勾股定理得:FG2+EF2=EG2,即x2+42=(2x)2,解得x=![]() ,
,
∵四边形BHGE是矩形
则HB=GE=![]() cm,
cm,
∴CH=BCBH=BCEG=(9![]() )cm,
)cm,
又在直角三角形CHG中,∠C=60°
则EB=GH=CHtan60°=(9![]() )×
)×![]() cm.
cm.
所以,t=(9![]() )秒.
)秒.
![]() 由于
由于![]() ,所以,点
,所以,点![]() 在边
在边![]() 上
上
如图所示,连结![]() ,则
,则![]()
由勾股定理得,![]() 2+
2+![]() 2=
2=![]() 2,
2,
过点D作DG⊥BC于G点
∴CG=BC-BG=BC-AD=6cm
∵∠C=60°
∴DG=CGtan60°=6![]() cm=AB
cm=AB
∴![]() =
=![]()
故![]() ,即
,即![]()
解得![]() (不合题意,舍去)
(不合题意,舍去)
所以,经过![]() 秒
秒![]() 与
与![]() 外切.
外切.


 名校课堂系列答案
名校课堂系列答案