Question

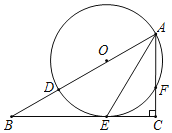
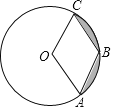
【题目】如图，已知⊙O的半径是2，点A、B、C在⊙O上，若四边形OABC为菱形，则图中阴影部分面积为（　　）

A. π﹣2 B. π﹣ C. π﹣2 D. π﹣

Answer 1

【答案】C

【解析】连接OB和AC交于点D，根据菱形及直角三角形的性质先求出AC的长及∠AOC的度数，然后求出菱形ABCO及扇形AOC的面积，则由S菱形ABCO﹣S扇形AOC可得答案．

连接OB和AC交于点D，如图所示：

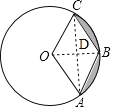
∵圆的半径为2，

∴OB=OA=OC=2，

又四边形OABC是菱形，

∴OB⊥AC，OD=OB=1，

在Rt△COD中利用勾股定理可知：CD=，AC=2CD=2，

∵sin∠COD= ，

∴∠COD=60°，∠AOC=2∠COD=120°，

∴S菱形ABCO=B×AC=×2×2=2，

S扇形AOC=，

则图中阴影部分面积为S菱形ABCO﹣S扇形AOC=，

故选：C．