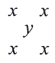题目内容
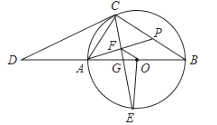
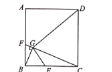
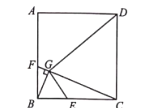
【题目】如图，在正方形
中，
分别是边
上的点，且满足
，连接
，过点B作
，垂足为点G，连接DG，则下列说法不正确的是（ ）
A.
B.
C.
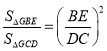D.
【答案】B
【解析】
根据正方形的性质、等角的余角相等即可判断A正确；根据B选项，判断出E为BC中点，与原题条件不一致，判断B错误；证明
，判断C选项正确；根据，得出
，判断D正确．
解：
四边形
是正方形，
，即
，
，
，
，
∴
选项正确，不合题意；
∵BG⊥CF，
∴∠BGC=90°，
∴∠GBC+∠BCG=90°, ∠BGE+∠CGE=90°，
当GE=BE时，∠BGE=∠GBE，
∴∠EGC=∠ECG，
∴GE=CE，
∴BE=CE，
即E为BC中点，
原题没有此条件，∴B选项不正确，符合题意；
，
，
∴∠FBG+∠CBG=90°, ∠FBG+∠BFG=90°,
∴∠CBG=∠BFG，
，
，
，
，
，又
，
，
，
∴
选项正确，不合题意；
，
，
，
，即
，
∴
选项正确，不合题意；
故选：
．
练习册系列答案
相关题目
【题目】观察下表：
序号 | 1 | 2 | 3 | … |
图形 |
|
|
| … |
我们把某格中字母和所得到的多项式称为特征多项式，例如：
第1格的“特征多项式”为
；
第2格的“特征多项式”为
．
回答下列问题：
（1）第3格的“特征多项式”为________________，
第4格的“特征多项式”为______________________，
第
格的“特征多项式”为___________________；
（2）若第1格的“特征多项式”的值为
，第2格的“特征多项式”的值为
，求
的值；
（3）在（2）的条件下，第格的特征多项式的值为
，则直接写出的值；若没有，请说明理由．
