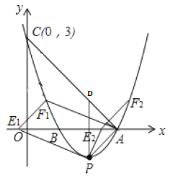
题目内容
【题目】如图，已知抛物线
的顶点坐标为
，且与
轴交于点C
，与
轴交于A、B两点（点A在点B的右侧）．
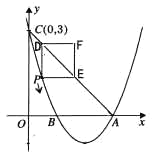
（1）求该抛物线的函数关系式；
（2）点P是该抛物线上一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥轴，交直线AC于点D；作PE∥x轴，交直线AC于点E，以PD，PE为边的矩形PEFD，问矩形PEFD周长是否存在最大值？若存在，求出此时P点的坐标及最大值；若不存在，请说明理由；
（3）在问题（2）的条件下，P点满足∠DAP=90°，且点E在轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由．
【答案】（1）y＝x24x＋3（2）存在，当P（
，-
），矩形PEFD周长最大值为9（3）F1（2
，1），F2（2＋，1）．
【解析】
（1）已知了抛物线的顶点坐标，可将抛物线的解析式设为顶点式，然后将函数图象经过的C点坐标代入上式中，即可求出抛物线的解析式；
（2）先求出A点坐标，可知△AOC是等腰直角三角形，再求出直线AC的解析式，由题意可知矩形PEFD为正方形，故矩形PEFD周长等于4DP，设P（x, x24x＋3）,再表示出D点坐标及DP的长，根据二次函数的性质即可求出最大值；
（3）根据∠DAP=90°，过P点作AP⊥AC于抛物线的交点即为P点，根据平行四边形的性质知：P、F的纵坐标互为相反数，可据此求出F点的纵坐标，代入抛物线的解析式中即可求出F点的坐标．
（1）∵抛物线的顶点为（2，1），
∴设抛物线的解析式为y＝a（x2）21，
将C（0，3）代入上式，得：
3＝a（02）21，a＝1；
∴y＝（x2）21，即y＝x24x＋3；
（2）令y=0，即x24x＋3=0
解得x1=1,x2=3
∴A（3,0）
∴CO=AO
∴△AOC是等腰直角三角形，∠CAO=45°
设直线AC的解析式为y=kx+b（k≠0），
把A（3,0），C（0，3）代入得
解得
∴直线AC的解析式为y=-x+3
∵PE∥x轴，
∴∠DPE=∠CAO=45°
∴∠EDP=90°-∠DPE=45°
∴DP=PE
故矩形PEFD为正方形，
设P（x, x24x＋3）,则D（x，-x+3）
∴DP=（-x+3）-（x24x＋3）=-x2+3x
∴矩形PEFD周长C=4DP=-4x2+12x=-4(x2-3x)= -4(x-)2+9
故存在当x=时，即P（，-），矩形PEFD周长最大值为9；
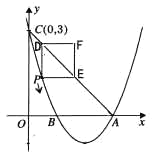
（3）如图，过P点作AP⊥AC于抛物线的交点即为P点，此时∠DAP=90°，
∵直线AC的解析式为y=-x+3
∴可设直线AP的解析为y=x+p
把A（3,0）代入得0=3+p
解得p=-3
∴直线AP的解析为y=x-3
联立
解得x1=3,y=0或x=2，y=-1
∴P（2,-1）
∵A、P、E、F为顶点的平行四边形
∴P、F的纵坐标互为相反数，
∴可设F（x，1），代入抛物线可得x24x＋3＝1，
解得x1＝2，x2＝2＋；
∴符合条件的F点有两个，
即F1（2，1），F2（2＋，1）．
