题目内容
【题目】已知锐角△ABC内接于圆O,D为弧AC上一点,分别连接AD、BD、CD,且∠ACB=90°﹣![]() ∠BAD.
∠BAD.
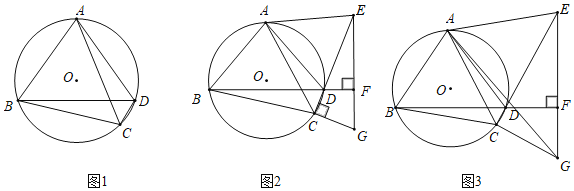
(1)如图1,求证:AB=AD;
(2)如图2,在CD延长线上取点E,连接AE,使AE=AD,过E作EF垂直BD的延长线于点F,过C作CG⊥EC交EF延长线于点G,设圆O半径为r,求证:EG=2r;
(3)如图3,在(2)的条件下,连接DG,若AC=BC,DE=4CD,当△ACD的面积为10时,求DG的长度.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)欲证明AB=AD,只要证明∠ABD=∠ADB即可;(2)如图2中,连接BE交AC于L,连接AO,延长AO交BD于J,交BE于T,连接CO,延长CO交⊙O于K,连接BK.想办法证明△CBK≌△ECG(AAS)可得结论;(3)如图3中,在图2的基础上作AH⊥DE于H.假设CD=k,DE=4k,则CE=CB=CA=5k,利用勾股定理求出AH,再利用三角形的面积公式求出K的值,再求出EG,CG即可解决问题.
(1)证明:如图1中,
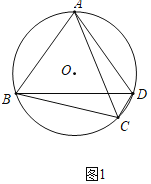
∵∠∠ADB=∠ACB,∠ACB=90°﹣![]() ∠BAD,
∠BAD,
∴∠ADB=90°﹣![]() BAD,
BAD,
∵∠ABD=180°﹣∠BAD﹣(90°﹣![]() ∠BAD)=90°﹣
∠BAD)=90°﹣![]() ∠BAD,
∠BAD,
∴∠ABD=∠ADB,
∴AB=AD.
(2)证明:如图2中,连接BE交AC于L,连接AO,延长AO交BD于J,交BE于T,连接CO,延长CO交⊙O于K,连接BK.
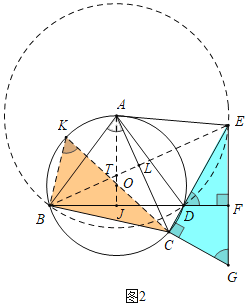
∵AE=AD,
∴∠ADE=∠AED,
∵∠ADE+∠ADC=180°,∠ADC+∠ABC=180°,
∴∠ADE=∠ABC=∠AED,
∵AB=AD,
∴![]() ,
,
∴∠ACB=∠ACE,AJ⊥BD,
∵AC=AC,
∴△ACB≌△ACE(AAS),
∴CB=CE,
∵AB=AE,
∴AC⊥BE,
∴∠ALB=∠AJB=90°,
∵∠ATL=∠BTJ,
∴∠TAL=∠TBJ,
∵AB=AD=AE,
∴∠BED=![]() ∠BAD=∠BAJ,
∠BAD=∠BAJ,
∵∠EDF=∠DBE+∠DEB,
∴∠EDF=∠BAC,
∵∠K=∠BAC,
∴∠K=∠EDF,
∵CG⊥CE.EG⊥BF,
∴∠DFE=∠GCG=90°,
∵∠DEF+∠EDF=90°,∠DEF+∠G=90°,
∴∠G=∠EDF=∠K,
∵∠CBK=∠GCE=90°,
∴△CBK≌△ECG(AAS),
∴EG=CK=2r,
(3)解:如图3中,在图2的基础上作AH⊥DE于H.
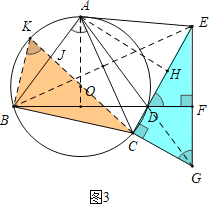
∵DE=4CD,
∴可以假设CD=k,DE=4k,则CE=CB=CA=5k,
∵AE=AD,AH⊥DE,
∴DH=EH=2k,CH=CD+DH=3k,
∴AH=![]() ,
,
AD=![]()
∵S△ACD=![]() CDAH=
CDAH=![]() k4k=10,
k4k=10,
∴k=![]() (负根舍弃),
(负根舍弃),
∴CD=![]() ,AC=BC=EC=5
,AC=BC=EC=5![]() ,AD=AB=10,
,AD=AB=10,
设CK交AB于J,OA=OC=r,则BJ=AJ=5,CJ=![]()
在Rt△AOJ中,则有r2=52+(10﹣r)2,
解得r=![]() ,
,
∴EG=2r=![]() ,
,
∴CG=![]()
∴DG=![]()