题目内容
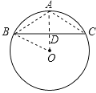
【题目】已知ABC内接于⊙O，且AB=AC，⊙O的半径为6cm ,点O到BC的距离为2cm,求AB的长.
【答案】
或
【解析】
根据A点所在的位置分类讨论：①若等腰三角形的顶点A在优弧BC上时，连接AO并延长交BC于点D，利用A、O都在BC中垂线上可得AO垂直平分BC，再利用勾股定理求出BD，从而求出AB；②若等腰三角形的顶点A在劣弧BC上时，连接AO交BC于点D，原理同上.
解：①若等腰三角形的顶点A在优弧BC上时，连接AO并延长交BC于点D，
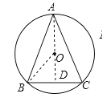
∵AB=AC
∴点A在BC的中垂线上
∵圆心O也在BC中垂线上，根据两点确定一条直线
∴AO垂直平分BC
∵⊙O的半径为6cm ,点O到BC的距离为2cm
∴OA=OB=6,OD=2
∴AD=8
根据勾股定理：
∴再根据勾股定理：
；
②若等腰三角形的顶点A在劣弧BC上时，连接AO交BC于点D
∵AB=AC
∴点A在BC的中垂线上
∵圆心O也在BC中垂线上，根据两点确定一条直线
∴AO垂直平分BC
∵⊙O的半径为6cm ,点O到BC的距离为2cm
∴OA=OB=6,OD=2
∴AD=4
根据勾股定理：
∴再根据勾股定理：
；
综上所述：或
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
