Question

【题目】已知在Rt△ABC中，∠ACB=90°，现按如下步骤作图：

①分别以A，C为圆心，a为半径（a＞AC）作弧，两弧分别交于M，N两点；

②过M，N两点作直线MN交AB于点D，交AC于点E；

③将△ADE绕点E顺时针旋转180°，设点D的像为点F．

（1）请在图中直线标出点F并连接CF；

（2）求证：四边形BCFD是平行四边形；

（3）当∠B为多少度时，四边形BCFD是菱形．

Answer 1

【答案】见解析；见解析；60°

【解析】

试题（1）根据题意作出图形即可；

（2）首先根据作图得到MN是AC的垂直平分线，然后得到DE等于BC的一半，从而得到DE=EF，即DF=BC，然后利用一组对边平行且相等的四边形是平行四边形进行判定即可；

（3）得到BD=CB后利用邻边相等的平行四边形是菱形进行判定即可

试题解析：（1）如图所示：

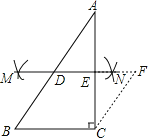
（2）∵根据作图可知：MN垂直平分线段AC，∴D、E为线段AB和AC的中点，

∴DE是△ABC的中位线，∴DE=BC，

∵将△ADE绕点E顺时针旋转180°，点D的像为点F， ∴EF=ED， ∴DF=BC，

∵DE∥BC， ∴四边形BCFD是平行四边形；

（3）当∠B=60°时，四边形BCFD是菱形； ∵∠B=60°， ∴BC=AB，

∵DB=AB， ∴DB=CB， ∵四边形BCFD是平行四边形， ∴四边形BCFD是菱形．