Question

【题目】正方形ABCD的边长为3，点E为射线AD上一点连接CE，设直线CE与BD交于点F，若AD＝2DE，则BF的长为_____．

Answer 1

【答案】6或2

【解析】

分两种情况：如图1，当DE在AD的延长线上时，②如图2，当DE在线段AD上时，根据正方形的性质和相似三角形的判定和性质定理即可得到结论．

解：①如图1，当DE在AD的延长线上时，

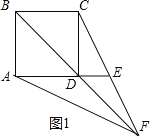
∵四边形ABCD是正方形，

∴AB＝AD＝BC＝3，

∴BD＝AB＝3，

∵AD＝2DE，

∴DE＝BC，

∵DE∥BC，

∴△FED∽△FCB，

∴

∴BF＝2DF＝2BD＝6；

②如图2，当DE在线段AD上时，

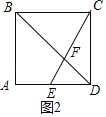
∵四边形ABCD是正方形，

∴AB＝AD＝BC＝3，

∴BD＝AB＝3，

∵AD＝2DE，

∴DE＝BC，

∵DE∥BC，

∴△FED∽△FCB，

∴，

∴BF＝2DF＝BD＝2，

综上所述，BF的长为6或2

故答案为：6或2．