题目内容
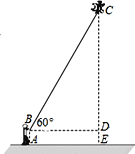
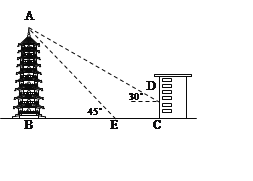
【题目】某风景区内有一古塔AB,在塔的北面有一建筑物,当光线与水平面的夹角是30°时,塔在建筑物的墙上留下了高3米的影子CD;而当光线与地面的夹角是45°时,塔尖A在地面上的影子E与墙角C有15米的距离(B、E、C在一条直线上),求塔AB的高度(结果保留根号).
【答案】塔AB的高度(12+9![]() )米.
)米.
【解析】
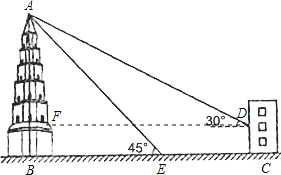
过点D作DF⊥AB,则图中有两个直角三角形即△ABE和△AFD,若假设AB=x米,则在△ABE中可求出BE,又EC已知,所以BC的值就确定了为x+15,在△AFD中,DF=AFcot30°=3(x-3),所以根据BC=DF则可列方程,只需解方程即可求值.
如图,过点D作DF⊥AB,垂足为F,
∵AB⊥BC,CD⊥BC,
∴四边形BCDF的矩形,
∴BC=DF,CD=BF,
设AB=x米,在Rt△ABE中,∠AEB=∠BAE=45°,
∴BE=AB=x,
在Rt△ADF中,∠ADF=30°,AF=AB-BF=x-3,
∴DF=AFcot30°=![]() (x-3),
(x-3),
∵DF=BC=BE+EC,
∴![]() (x-3)=x+15,
(x-3)=x+15,
解得x=12+9![]() ,
,
答:塔AB的高度(12+9![]() )米.
)米.

练习册系列答案
相关题目