题目内容
如图,⊙O与⊙P相交于B、C两点,BC是⊙P的直径,且把⊙O分成度数的比为1:2的两条弧,A是
上的动点(不与B、C重合),连接AB、AC分别交⊙P于D、E两点.
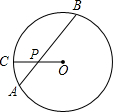
(1)当△ABC是锐角三角形(图①)时,判断△PDE的形状,并证明你的结论;
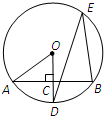
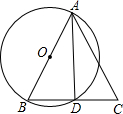
(2)当△ABC是直角三角形、钝角三角形时,请你分别在图②、图③中画出相应的图形(不要求尺规作图),并按图①标记字母;
(3)在你所画的图形中,(1)的结论是否成立?请就钝角的情况加以证明.

 |
| BmC |
(1)当△ABC是锐角三角形(图①)时,判断△PDE的形状,并证明你的结论;
(2)当△ABC是直角三角形、钝角三角形时,请你分别在图②、图③中画出相应的图形(不要求尺规作图),并按图①标记字母;
(3)在你所画的图形中,(1)的结论是否成立?请就钝角的情况加以证明.

(1)△PDE是等边三角形,连DC.
∵弦BC把⊙O分成度数的比为1:2的两条弧,
∴
的度数为120°,
∴∠BAC=60°
又∵BC为⊙P的直径,∴∠BDC=90°,
又∵∠A=60°,
∴∠DCA=30°,
∴∠DPE=60°
又∵PD=PE,
∴△PDE是等边三角形;
(2)如图②、图③即为所画图形;
(3)图②和图③中△PDE仍为等边三角形.
证明:如图③,连接BE、DC
∵BC为⊙P的直径,
∴∠BDC=90°
又∵∠A=60°,
∴∠ACD=30°
又∵四边形DBEC是⊙P的内接四边形,
∴∠DBE=∠DCA=30°,∠DPE=60°
又∵PD=PE,
∴△PDE是等边三角形.

∵弦BC把⊙O分成度数的比为1:2的两条弧,
∴
 |
| BC |
∴∠BAC=60°
又∵BC为⊙P的直径,∴∠BDC=90°,
又∵∠A=60°,
∴∠DCA=30°,
∴∠DPE=60°
又∵PD=PE,
∴△PDE是等边三角形;
(2)如图②、图③即为所画图形;
(3)图②和图③中△PDE仍为等边三角形.
证明:如图③,连接BE、DC
∵BC为⊙P的直径,
∴∠BDC=90°
又∵∠A=60°,
∴∠ACD=30°
又∵四边形DBEC是⊙P的内接四边形,
∴∠DBE=∠DCA=30°,∠DPE=60°
又∵PD=PE,
∴△PDE是等边三角形.


练习册系列答案
相关题目