ĢāÄæÄŚČŻ
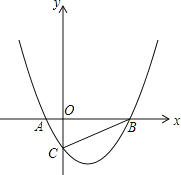
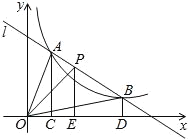
”¾ĢāÄæ”æ¶ŌÓŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠµÄµćPŗĶ”ŃC£¬øų³öČēĻĀµÄ¶ØŅå£ŗČō”ŃCÉĻ“ęŌŚĮ½øöµćA”¢B£¬Ź¹µĆ”ĻAPB£½60”ć£¬Ōņ³ĘPĪŖ”ŃCµÄæÉŹÓµć£®
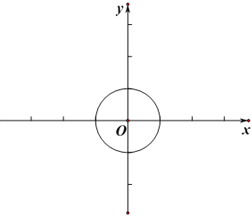
£Ø1£©µ±”ŃOµÄ°ė¾¶ĪŖ1Ź±£¬
¢ŁŌŚµć![]() ”¢E(1£¬1)”¢F(3£¬0)ÖŠ£¬”ŃOµÄæÉŹÓµćŹĒ______£®
”¢E(1£¬1)”¢F(3£¬0)ÖŠ£¬”ŃOµÄæÉŹÓµćŹĒ______£®
¢Ś¹żµćM(4£¬0)×÷Ö±Ļßl£ŗy=kx+b£¬ČōÖ±ĻßlÉĻ“ęŌŚ”ŃOµÄæÉŹÓµć£¬ĒóbµÄȔֵ·¶Ī§£»
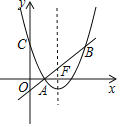
£Ø2£©ČōT(t£¬0)£¬”ŃTµÄ°ė¾¶ĪŖ1£¬Ö±Ļßy=![]() ÉĻ“ęŌŚ”ŃTµÄæÉŹÓµć£¬ĒŅĖłÓŠæÉŹÓµć¹¹³ÉµÄĻ߶Ī³¤¶ČĪŖn£¬Čō
ÉĻ“ęŌŚ”ŃTµÄæÉŹÓµć£¬ĒŅĖłÓŠæÉŹÓµć¹¹³ÉµÄĻ߶Ī³¤¶ČĪŖn£¬Čō![]() £¬Ö±½ÓŠ“³öt µÄȔֵ·¶Ī§£®
£¬Ö±½ÓŠ“³öt µÄȔֵ·¶Ī§£®
”¾“š°ø”æ£Ø1£©¢ŁD”¢E£¬¢Ś![]() £»£Ø2£©
£»£Ø2£©![]() »ņ
»ņ![]()
”¾½āĪö”æ
£Ø1£©¢Łøł¾ŻĢāŅā¾ŁĄżĖµĆ÷¼“æÉ£»
¢Śµ±Ö±ĻßlÓė°ė¾¶ĪŖ2µÄ”ŃOĻąĒŠŹ±£¬ĄūÓĆsin”ĻAMO£½![]() £¬æÉĒóµĆ”ĻAMO£½30”ć£¬½ų¶ųæÉĒóµĆOE³¤£¬“Ó¶ųæɵĆbµÄȔֵ·¶Ī§£»
£¬æÉĒóµĆ”ĻAMO£½30”ć£¬½ų¶ųæÉĒóµĆOE³¤£¬“Ó¶ųæɵĆbµÄȔֵ·¶Ī§£»
£Ø2£©µ±t£¾0Ź±£¬ĻČĒóÖ±Ļßy£½![]() Óė°ė¾¶ĪŖ2µÄ”ŃTĻąĒŠŹ±µÄtµÄÖµ£¬ŌŁĒóÖ±Ļßy£½
Óė°ė¾¶ĪŖ2µÄ”ŃTĻąĒŠŹ±µÄtµÄÖµ£¬ŌŁĒóÖ±Ļßy£½![]() Óė°ė¾¶ĪŖ2µÄ”ŃTĻą½»ĒŅĖł½ŲĻ߶Ī³¤ĪŖ
Óė°ė¾¶ĪŖ2µÄ”ŃTĻą½»ĒŅĖł½ŲĻ߶Ī³¤ĪŖ![]() Ź±µÄtµÄÖµ£¬½ų¶ųĒóµĆtµÄȔֵ·¶Ī§£®
Ź±µÄtµÄÖµ£¬½ų¶ųĒóµĆtµÄȔֵ·¶Ī§£®
½ā£ŗ£Ø1£©¢ŁČēĶ¼£¬¹żµćD×÷DA”ĪxÖį£¬DB”ĪyÖį£¬æɵƔĻADB£½90”ć£¬µ±µćA”¢BŌŚŌ²ÉĻŌ½Ą“Ō½ææ½üŹ±£¬”ĻADBæÉŅŌĪŖ60”ć£¬ŌņµćDŹĒæÉŹÓµć£»
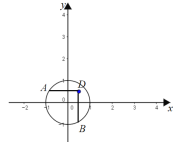
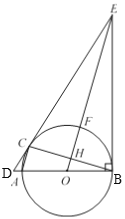
ČēĶ¼£¬¹żµćE×÷”ŃOµÄĒŠĻßEA”¢EB£¬Ōņ”ĻOAE£½”ĻOBE £½90”ć
Ó֔ߔĻAOB£½90”ć£¬”ą”ĻE£½90”ć£¬
µ±µćA”¢BŌŚŌ²ÉĻŌ½Ą“Ō½ææ½üŹ±£¬”ĻAEBæÉŅŌĪŖ60”ć£¬ŌņµćEŹĒæÉŹÓµć£»
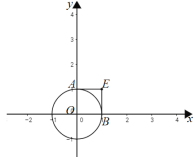
ÓÉĢāŅāæÉÖŖ£¬µ±µćPŌŚ”ŃOĶāŹ±£¬¹żµćP×÷”ŃOµÄĒŠĻßPA”¢PB£¬Ōņ“ĖŹ±”ĻAPB×ī“ó£¬Čō”ĻAPB”Ż60”ć£¬Ōņ”ŃOÉĻŅ»¶Ø“ęŌŚĮ½øöµćA”¢B£¬Ź¹µĆ”ĻAPB£½60”ć£®
ČēĶ¼£¬¹żµćP×÷”ŃOµÄĒŠĻßPA”¢PB£¬µ±”ĻAPB£½60”揱£¬Ōņ”ĻAPO£½”ĻBPO£½30”ć£¬
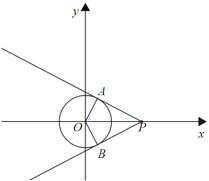
ŌŚRt”÷AOPÖŠ£¬sin”ĻAPO£½![]() £¬
£¬
”ßOA£½1£¬
”ąOP£½2
”ąµ±OP”Ü2Ź±£¬”ŃOŅ»¶ØÓŠæÉŹÓµć£¬µ±OP£¾2Ź±£¬”ŃOƻӊæÉŹÓµć£®
”ßµćF£Ø3,0£©£¬
”ąOF£½3£¾2£¬
”ąµćF²»ŹĒæÉŹÓµć
¹Ź“š°øĪŖ£ŗD”¢E£®
¢ŚÓÉ¢ŁµĆ£¬ČōÖ±ĻßlÉĻ“ęŌŚ”ŃOµÄæÉŹÓµć£¬ŌņÖ±ĻßlÓė°ė¾¶ĪŖ2µÄ”ŃOĻąĒŠ»ņĻą½»£»
ČēĶ¼£¬µ±Ö±ĻßlÓė°ė¾¶ĪŖ2µÄ”ŃOĻąĒŠŹ±£¬
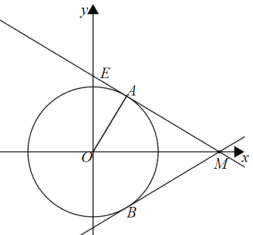
”ßM(4£¬0)£¬
”ąOM£½4£¬
”ąŌŚRt”÷AOMÖŠ£¬sin”ĻAMO£½![]() £¬
£¬
”ą”ĻAMO£½30”ć£¬
”ąŌŚRt”÷EOMÖŠ£¬tan”ĻEMO£½![]() £¬
£¬
”ą![]() £¬
£¬
”ąČōÖ±ĻßlÉĻ“ęŌŚ”ŃOµÄæÉŹÓµć£¬ĒóbµÄȔֵ·¶Ī§ĪŖ![]() £»
£»
£Ø2£©µ±y£½0Ź±£¬![]() £½0£¬
£½0£¬
½āµĆ£¬x£½![]() £¬ŌņÖ±ĻßlÓėxÖįµÄ½»µć×ų±źĪŖ£Ø
£¬ŌņÖ±ĻßlÓėxÖįµÄ½»µć×ų±źĪŖ£Ø![]() £¬0£©£¬
£¬0£©£¬
µ±x£½0Ź±£¬y£½![]() £¬ŌņÖ±ĻßlÓėyÖįµÄ½»µć×ų±źĪŖ£Ø0£¬
£¬ŌņÖ±ĻßlÓėyÖįµÄ½»µć×ų±źĪŖ£Ø0£¬![]() £©£¬
£©£¬
”ßÖ±Ļßy£½![]() ÉĻ“ęŌŚ”ŃTµÄæÉŹÓµć£¬ĒŅ”ŃTµÄ°ė¾¶ĪŖ1£¬
ÉĻ“ęŌŚ”ŃTµÄæÉŹÓµć£¬ĒŅ”ŃTµÄ°ė¾¶ĪŖ1£¬
”ąÖ±Ļßy£½![]() Óė°ė¾¶ĪŖ2µÄ”ŃTĻą½»»ņĻąĒŠ
Óė°ė¾¶ĪŖ2µÄ”ŃTĻą½»»ņĻąĒŠ
µ±t£¾0Ź±£¬
ČēĶ¼£¬µ±Ö±Ļßy£½![]() Óė°ė¾¶ĪŖ2µÄ”ŃTĻąĒŠŹ±£¬
Óė°ė¾¶ĪŖ2µÄ”ŃTĻąĒŠŹ±£¬
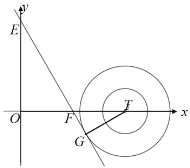
”ßE£Ø0£¬![]() £©£¬F£Ø
£©£¬F£Ø![]() £¬0£©£¬
£¬0£©£¬
”ąOE£½![]() £¬OF£½
£¬OF£½![]() £¬
£¬
”ąŌŚRt”÷EOFÖŠ£¬tan”ĻEFO£½ £¬
£¬
”ą”ĻTFG£½”ĻEFO£½60”ć£¬
”ßT£Øt£¬0£©£¬
”ąTF£½![]() £¬
£¬
”ąŌŚRt”÷TGFÖŠ£¬sin”ĻTFG£½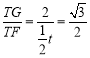 £¬
£¬
”ą![]() £¬
£¬
ČēĶ¼£¬µ±Ö±Ļßy£½![]() Óė°ė¾¶ĪŖ2µÄ”ŃTĻą½»ĒŅCD£½
Óė°ė¾¶ĪŖ2µÄ”ŃTĻą½»ĒŅCD£½![]() Ź±£¬
Ź±£¬
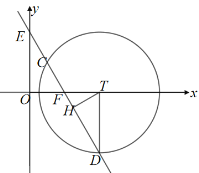
¹żµćT×÷TH”ĶCD£¬Ōņ![]()
ŌŚRt”÷THDÖŠ£¬cos”ĻTDH£½![]() £¬
£¬
”ą”ĻTDH£½30”ć£¬
Ó֔ߔĻTFD£½60”ć£¬
”ą”ĻDTF£½90”ć£¬
”ąŌŚRt”÷TFDÖŠ£¬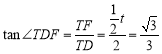 £¬
£¬
”ą![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬
£¬
Ķ¬Ąķ£¬µ±t£¼0Ź±£¬![]()
×ŪÉĻĖłŹö£¬tµÄȔֵ·¶Ī§ĪŖ£ŗ![]() »ņ
»ņ![]()