题目内容
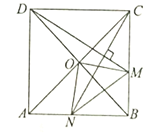
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 与
与![]() 的交点,
的交点,![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .下列四个结论:①
.下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 的最小值是1.其中正确结论是( )
的最小值是1.其中正确结论是( )
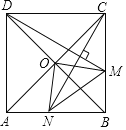
A.①②③B.①③④C.①②④D.②③④
【答案】A
【解析】
根据正方形的性质,依次判定△CNB≌△DMC,△AON≌△BOM,△OCM≌△OBN,![]() ,根据全等三角形的性质以及勾股定理进行计算即可得出结论.
,根据全等三角形的性质以及勾股定理进行计算即可得出结论.
∵正方形ABCD中,CD=BC,∠BCD=90![]() ,
,
∴∠BCN+∠DCN=90![]() ,
,
又∵CN⊥DM,
∴∠CDM+∠DCN=90![]() ,
,
∴∠BCN=∠CDM,
又∵∠CBN=∠DCM=90![]() ,
,
∴△CNB≌△DMC(ASA),
∴BN=CM,
故AN=BM
∵AO=BO,∠OAN=∠OBM=45°,
∴△AON≌△BOM,
∵BO=CO,∠OCM=∠OBN =45°,
∴△OCM≌△OBN,
∴![]() =S△OBN+ S△BOM= S△OBN+S△AON=S△AOB=
=S△OBN+ S△BOM= S△OBN+S△AON=S△AOB=![]()
![]()
即![]() ,①正确;
,①正确;
∵△AON≌△BOM,
∵∠MON=∠BOM+∠BON=∠AON +∠BON=90°,ON=OM
∴△MNO是等腰直角三角形,
∴MN=![]()
∵△MNB是直角三角形,
∴![]()
又CM=BN
∴![]()
即![]() ,②正确;
,②正确;
∵∠CON=90°+∠BON, ∠DOM=90°+∠COM,∠BON=∠COM
∴∠CON=∠DOM
又CO=DO, ON=OM,
∴![]() ,③正确;
,③正确;
④∵AB=2,
∴S正方形ABCD=4,
∵△OCM≌△OBN,
∴四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1,
∴当△MNB的面积最大时,△MNO的面积最小,
设BN=x=CM,则BM=2x,
∴△MNB的面积=![]() x(2x)=
x(2x)= ![]() x2+x=
x2+x= ![]() (x1)2+
(x1)2+![]() ,
,
∴当x=1时,△MNB的面积有最大值![]() ,
,
此时S△OMN的最小值是1 ![]() =
=![]() ,
,
故④不正确;