题目内容
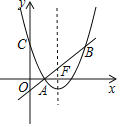
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,0),B两点,与y轴交于C(0,3),对称轴为直线x=2.
(1)请直接写出该抛物线的解析式;
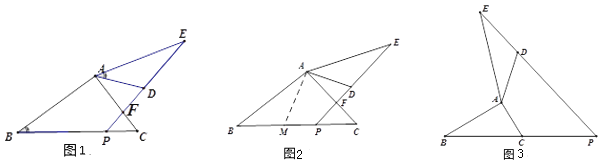
(2)设直线l与抛物线的对称轴的交点为F,在对称轴右侧的抛物线上有一点G,若![]() ,且S△BAG=6,求点G的坐标;
,且S△BAG=6,求点G的坐标;
(3)若在直线![]() 上有且只有一点P,使∠APB=90°,求k的值.
上有且只有一点P,使∠APB=90°,求k的值.
【答案】(1)y=x2﹣4x+3;(2)G(5,8);(3)k=![]()
【解析】
(1)抛物线与x轴另外一个交点坐标为(3,0),则函数的表达式为:y=a(x﹣1)(x﹣3)=a(x2﹣4x+3),即:3a=3,即可求解;
(2)分点G在点B下方、点G在点B上方两种情况,分别求解即可;
(3)由△PAS∽△BPT,则![]() ,即可求解.
,即可求解.
解:(1)![]() ,
,![]() 两点,对称轴为直线
两点,对称轴为直线![]() ,则抛物线与
,则抛物线与![]() 轴另外一个交点坐标为
轴另外一个交点坐标为![]() ,
,
则函数的表达式为:![]() ,
,
即:![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:![]() ①;
①;
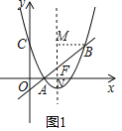
(2)过点![]() 作
作![]() 轴交对称轴于点
轴交对称轴于点![]() ,设对称轴与
,设对称轴与![]() 轴交于点
轴交于点![]() .
.
![]()
![]() ,
,
又![]() ,则
,则![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,则
,则![]() ,则
,则![]() ,
,
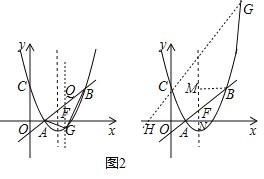
①若点![]() 在点
在点![]() 下方,则过点
下方,则过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,则设点
,则设点![]() ,
,![]() ,
,
![]() ,
,
即:![]() ,△
,△![]() ,无解;
,无解;
②若点![]() 在点
在点![]() 上方,则过点
上方,则过点![]() 作
作![]() 交
交![]() 轴于
轴于![]() ,则
,则![]() ,
,
即:![]() ,则
,则![]() ,则
,则![]() ,
,
则可设直线![]() 的解析式为:
的解析式为:![]() ,将
,将![]() 代入得,
代入得,![]() .
.
![]() 直线
直线![]() 的解析式为
的解析式为![]() ②,
②,
联立①②并解得:![]() 或5(舍去
或5(舍去![]() ,
,
![]() ;
;
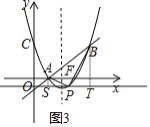
(3)分别过点![]() ,
,![]() 作直线
作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,
,![]() ,
,
则![]() ,则
,则![]() ,
,
直线![]() 的解析式为
的解析式为![]() ③,
③,
联立①③并解得:![]() 或
或![]() ,
,
则点![]() ,
,
设:![]() ,则
,则![]() 有两个相等实数根,
有两个相等实数根,
△![]() ,
,
解得:![]() (舍去负值),
(舍去负值),
故:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目